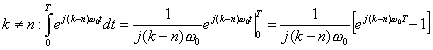
In the previous lesson, we used Euler's formula and trigonometric identities to determine the Fourier Series coefficients in our examples. Unfortunately, not all periodic signals are as convenient to work with as these were.
For general periodic signals, we need a method to find the Fourier Series coefficients Ck.
To do this, we will make use of this integral a lot (k and n are integers):
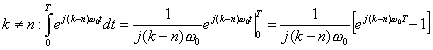
| Now, as always, | , so we get: |
| because | since this is just an integer multiple of 2π |
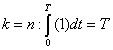
Therefore, we see that,
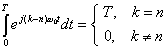
which is known as the "Orthogonality of Exponentials."
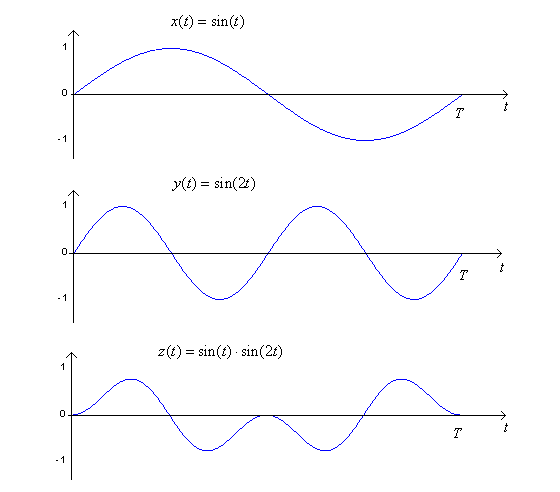
This figure demonstrates the orthogonality of exponentials. If we multiply x(t) = sin(t) by y(t) = sin(2t) and integrate z(t)= x(t) y(t) from 0 to T (over one period), it is clear that the integral of z(t) is 0 (just take the area under the curve).
We will use this to determine the Fourier Series coefficients Ck as follows:
| 1. Take | |
| 2. Multiply both sides of this equation by |
| 3. Integrate both sides of the equation over one period of the signal: |
![]()
Switching the order of the sum and integral in the second term (this is valid in all but pathological cases), we get
![]()
We've seen this integral before. We can pick any period over which to integrate our periodic signal. A convenient period is [0,T0).
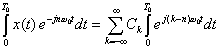
From above, we get
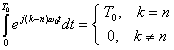
Therefore, we get
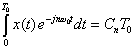
| because the only term that is nonzero in the sum | 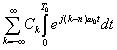 |
is for k=n. All other terms are 0. |
| Therefore, we can derive our Fourier Series coefficients Cn from our input periodic signal x(t) as | 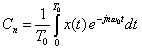 |
FINALLY, we can write our Fourier Series Pair as:
| For k = 0, | 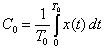 |
gives the DC value which is simply the average value of x(t) over one period. |
Example 1 Given a signal x(t) = cos(t) + sin(2t) , find its Fourier Series coefficients.
Example 2 Given a signal y(t) = cos(2t), find its Fourier Series coefficients.
Example 3 Given a periodic square wave

Find its Fourier Series coefficients.
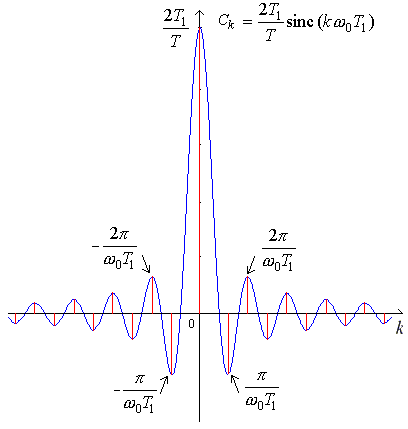
We can plot the frequency spectrum or line spectrum of a signal. It is a graph that shows the amplitudes and/or phases of the Fourier Series coefficients Ck. The plots are called line spectra because we indicate the values by lines.
| Example 4 Calculate the Fourier Series coefficients for the impulse train | |
| and plot the magnitude of its frequency spectrum (which are simply the | Fourier Series coefficients). |
Example 5 Calculate the Fourier Series coefficients for the periodic square wave and plot its frequency spectrum
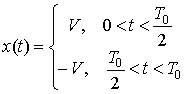
Notice that the spectrum for the square wave dies off as 1/k whereas for the periodic impulse train, it remains constant. We could approximate a periodic square wave with a finite number of Fourier Series terms. However, since all harmonics are important for the periodic impulse train, we could never build it in practice with just a finite number of terms.
Because the Fourier Series
![]()
has an infinite number of terms, we must consider if it converges. Further, we can approximate a signal x(t) to any degree of accuracy with a truncated Fourier Series.
The Fourier Series will converge (under a mean square error norm) if:

Any one of these conditions is sufficient for convergence.