The Laplace Transform

1. Using the Laplace Transform, differential equations can be solved algebraically.
2. We can use pole/zero diagrams from the Laplace Transform to determine the frequency response of a system and whether or not the system is stable.
3. We can transform more signals than we can with the Fourier Transform, because the Fourier Transform is a special case of the Laplace Transform.
4. The Laplace Transform is used for analog circuit design.
5. The Laplace Transform is used in Control Theory and Robotics

Definitions of Laplace Transform

The Bilateral Laplace Transform of a signal x(t) is defined as:

The complex variable s = σ + jω, where ω is the frequency variable of the Fourier Transform (simply set σ = 0). The Laplace Transform converges for more functions than the Fourier Transform since it could converge off of the jω axis. Here is a plot of the s-plane:

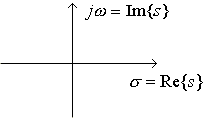
The Inverse Bilateral Laplace Transform of X(s) is:

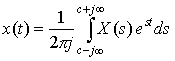
Notice that to compute the inverse Laplace Transform, it requires a contour integral. (When taking the inverse transform, the value of c for the contour integral must be in the region where the integral exists.) Fortunately, we will see more convenient ways (namely, Partial Fraction Expansion) to take the inverse transform so you are not required to know how to do contour integration.

If we define x(t) to be 0 for t < 0, this gives us the unilateral Laplace transform:

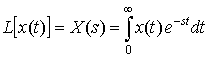
As we'll see, an important difference between the bilateral and unilateral Laplace Transforms is that you need to specify the region of convergence (ROC) for the bilateral case.

We point out (without proof) several features of ROCs:

• A right-sided time function (i.e. x(t) = 0, t < t₀ where t₀ is a constant) has an ROC that is a right half-plane.
• A left-sided time function has an ROC that is a left half-plane.
• A 2-sided time function has an ROC that is either a strip or else the ROC does not exist, which means that the Laplace Transform does not exist.
• If the ROC contains the jω- axis, then if x(t) were used as an impulse response, the system would be BIBO stable. If the boundary of the ROC is the jω-axis (i.e. Re(s) > 0 or Re(s) < 0), the system would be BIBO unstable.

  Taking the Laplace Transform is clearly a linear operation:

  L[ax₁(t) + bx₂(t)] = aX₁(s) + bX₂(s)

  where X₁(s) is the Laplace Transform of x₁(t) and X₂(s) is the Laplace Transform of x₂(t).

  Laplace Transform Examples

  Example 1 

  In Example 1, we needed to specify that Re(s) > 0. If this is not the case, the integral would have not converged at the upper limit of infinity.

  Example 2 

  The general Laplace Transform for an exponential function is:

  

Laplace Transforms of Functions

Example 3 

Example 4