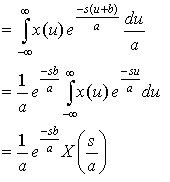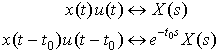
As we saw from the Fourier Transform, there are a number of properties that can simplify taking Laplace Transforms. I'll cover a few properties here and you can read about the rest in the textbook.
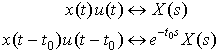
Derive this:
Plugging in the time-shifted version of the function into the Laplace Transform definition, we get:
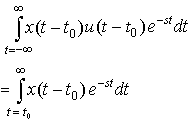
Letting τ = t - t0, we get:
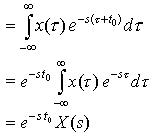
Example 1 Find the Laplace Transform of x(t) = sin[b(t - 2)]u(t - 2)

Recall the equation for the voltage of an inductor:
![]()
If we take the Laplace Transform of both sides of this equation, we get:
![]()
which is consistent with the fact that an inductor has impedance sL.
Proof of the Differentiation Property:
1) First write x(t) using the Inverse Laplace Transform formula:
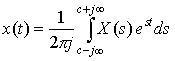
2) Then take the derivative of both sides of the equation with respect to t (this brings down a factor of s in the second term due to the exponential):
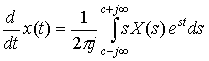
3) This shows that x
![]()
The Differentiation Property is useful for solving differential equations.
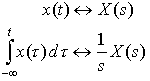
Recall the equation for the voltage of a capacitor turned on at time 0:
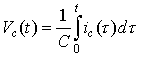
![]()
| which is consistent with the fact that a capacitor has impedance | . |
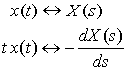
Derive this:
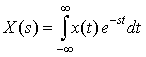
Take the derivative of both sides of this equation with respect to s:

This is the expression for the Laplace Transform of -t x(t). Therefore,
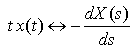
![]()
(Given without proof)
![]()
(Given without proof)
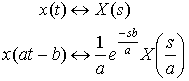
Derive this:
Plugging in the definition, we find the Laplace Transform of x(at -b):

Let u = at - b and du = adt, we get: