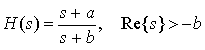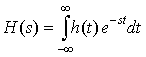
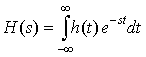
where h(t) is an impulse response, is called the system function or transfer function and it completely characterizes the input/output relationship of an LTI system. We can use it to determine time responses of LTI systems.
We can use Laplace Transforms to solve differential equations for systems (assuming the system is initially at rest for one-sided systems) of the form:
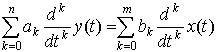
Taking the Laplace Transform of both sides of this equation and using the Differentiation Property, we get:
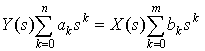
From this, we can define the transfer function H(s) as
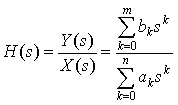
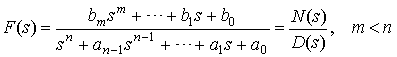
We write its Partial Fraction Expansion as:
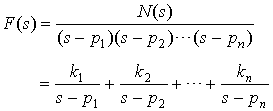
where
![]()
is the residue of the pole at pj.
Thus
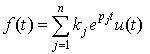
because the Inverse Laplace Transform of
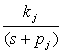
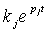
Example 1 Find y(t) where the transfer function H(s) and the input x(t) are given. Use Partial Fraction Expansion to find the output y(t):
![]()
Example 2 Find the transfer function H(s) for the differential equation. Assume zero initial conditions.
y'(t) + 2y(t) = 3x'(t).
Example 3 Now let the input to the system be x(t) = 5u(t). Find y(t).
As we saw for the Fourier Transform
x(t)*h(t) ↔ X(s)H(s)
This is useful for studying LTI systems. In fact, we can completely characterize an LTI system from:
Example 4 Find the step response s(t) to
h(t) = e-tu(t)
| Hint: |
Example 5 Find the output of an LTI system with impulse response h(t) = ebtu(t) to an input x(t) = eatu(t), where a ≠ b.
We saw that a condition for bounded-input bounded-output stability was:
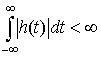
Let's look at stability from a system function standpoint. Given a Laplace Transform H(s), we expand H(s) with Partial Fraction Expansion:
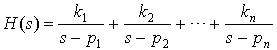
The corresponding impulse response is:
![]()
What happens to h(t) as t → ∞? For a system to be stable, its impulse response must not blow up as t → ∞.
| If Re{pi}, | , then h(t) decays to 0 as t → ∞ and the system is stable |  |
Therefore, the system is BIBO stable if and only if all poles of H(s) are in the left half plane of the s-plane.
If you study CONTROL THEORY, you will learn more about this. Using feedback , you can build systems to steer the poles into the left half plane and thus stabilize the system. Here is an example of such a system.
Example 6 FEEDBACK
h(t) = etu(t)
You can find the inverse of a system using Laplace Transforms. This is because:
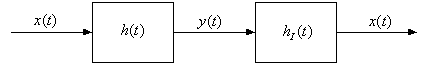
![]()
Take the Laplace Transform of both sides of this equation:
![]()
Therefore, the Laplace Transform of the inverse system is simply
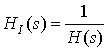
Example 7 Find the inverse system of