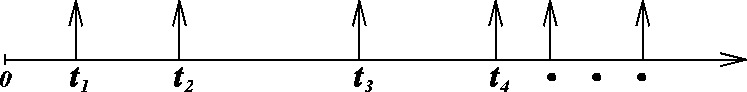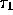 = the time until the next arrival.
= the time until the next arrival.
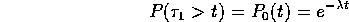

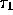 has an
exponential distribution!
has an
exponential distribution!
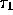 = the time until the next arrival.
= the time until the next arrival.
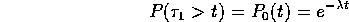

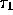 has an
exponential distribution!
has an
exponential distribution!
Let 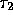 = the time between the first and second arrival
= the time between the first and second arrival
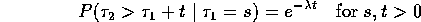
independently of 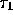 !
!
 as the time between the second and third arrival;
as the time between the second and third arrival;
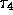 as the time between the third and fourth arrival; . . .
as the time between the third and fourth arrival; . . .
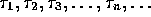 are called the
interarrival times of the Poisson process.
are called the
interarrival times of the Poisson process.
![]() The interarrival times,
The interarrival times,  , are
independent
of each other and each have an
exponential distribution
with mean
, are
independent
of each other and each have an
exponential distribution
with mean 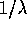 .
.