Analysis of IEEE 802.5 Token Ring Performance
© Copyright University of New Haven 1998
This analysis assumes "Early Release" of the token. Let:
µ
be mean frame service rate (1/DT)
lambda
be mean aggregate frame arrival rate at all stations
U
be channel efficiency; at equilibrium, U = rho = lambda/µ
q
be mean frame queue length at a station when the token arrives
N
be number of stations on the ring
DP
be propagation delay around cable
R
be data rate
TRT
be Token Rotation Time, the period between appearances of the token at a point in the ring
Token Rotation Time, TRT = cable propagation delay (DP) + (at least) 1-bit delay (1/R) at each of N stations + Station Service Time (q/µ) at each of N stations:
TRT = DP + N/R + qN/µ
assuming that the station service time, q/µ, is less than the Token Holding Time (THT) the Lightly Loaded case. The queue of frames which accumulates at a station in a period TRT is 1 N'th of the total number of frames which arrive at all stations:
q = TRT × lambda / N
Thus, substituting for q in the expression for TRT:
TRT = DP + N/R + TRT × lambda × N/(µ×N) = DP + N/R + rho × TRT
which can be re-arranged to give an expression for Token Rotation Time, TRT:
TRT = 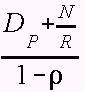
When a frame arrives at a station, it can expect to be about half way through a period of Token Rotation Time, and thus delay is on average, about ½TRT. As efficiency --> 1, TRT --> infinity.
In case of a system at equilibrium, q/µ<THT because each station clears its entire backlog of accumulated frames before the Token Holding Timer expires. Then:
U = 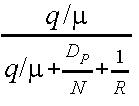 = rho
Lightly Loaded Case
= rho
Lightly Loaded Case
In case of a temporarily overloaded (i.e. non-equilibrium) system, where, q/µ>THT, channel efficiency, U < rho, because each station can not clear its entire backlog of accumulated frames. Then:
U = 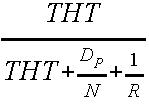 Heavily
Loaded Case
Heavily
Loaded Case
e.g. In a system at equilibrium, let N=100, R=10 Mbps, frame size = 1000 bits, DP=5 µsec, and mean aggregate frame arrival rate at all stations, lambda = 5000 frames/sec. Then, frame service time, 1/µ = DT = 1000/R = 100 µsecs and efficiency, rho = lambda / µ = 5000 × 100×10-6 = ½. Delay = ½TRT = ½ (5 + 100/10)/(1-½) = 15 µsec. A station's queue of backlogged frames, q = 30×10-6×5000/100 = 0.0015, giving station service time, q/µ = .0015×100 = 0.15 µsecs. Assuming that THT exceeds 0.15 µsecs, then the Lightly Loaded equation gives: efficiency, U = 0.15/(0.15+5/100+1/10) = ½. Assuming THT=1 millisecond, then the Heavily Loaded equation gives U = 1000/1000.15, very close to 1.