The Fourier Transform
Derivation
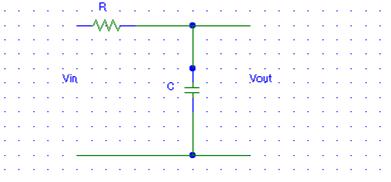
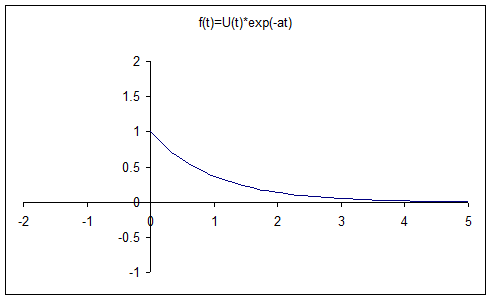
Assume that we have a generalized, time-limited pulse centered at t = 0 as shown below.
The Fourier Transform of this pulse can be developed by starting with a periodic version of this pulse where the original pulse now repeats every T seconds.
 Note:
Note:
![]()
fT(t) is periodic with period T so we can express it by its exponential Fourier series as
![]()
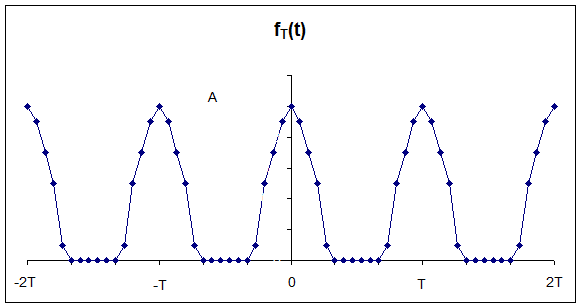
where

and
![]()
Now let’s make a small change in notation
1. wn = n*w0
2. F(wn) = T*Fn
We now have
![]() and
and 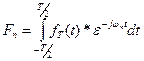
The sum can be rewritten as
![]()
or
![]()
![]() Taking the limit as T ¥
Taking the limit as T ¥
![]()
![]() But w0 = 2p/T so
for large T let w0 Dw and the limit becomes
But w0 = 2p/T so
for large T let w0 Dw and the limit becomes
![]()
![]()
![]() or since
T ¥ implies that Dw 0 and the sum, in the limit, becomes
an integral
or since
T ¥ implies that Dw 0 and the sum, in the limit, becomes
an integral
 and
and ![]()
This pair of equations defines the Fourier Transform
1. F(w) is the Fourier Transform of f(t)
2. f(t) is the inverse Fourier Transform of F(w)
3. F(w) is also called the Spectral Density of f(t) as it describes how the energy of the original pulse is distributed as a function of frequency (in radians per second)
I use a backwards upper case script “F” to denote taking the Fourier Transform of a function and the same symbol with a “-1” superscript to denote taking the inverse Fourier Transform.
Example 1
Take the Fourier Transform of the single-sided exponential
![]()
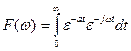
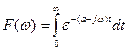
![]()
![]()
Note that the Fourier Transform is complex. It has a magnitude and a phase. The magnitude is found by multiplying it by its complex conjugate and taking the square root.
![]()
![]()
![]() This is the magnitude
This is the magnitude
Now find the phase. First, find the real and imaginary parts.
![]()
![]()
![]()
Therefore the real part is
![]()
and the imaginary part is
![]()
The phase is then given by
![]()
Note: The ArcTan function of your calculator can lie! Its answers always fall between ±90° (±π/2) and the real answer can be in one of the other
two quadrants. You should draw a picture
to adjust your result as required.
Singularity Functions
We run into special functions
when taking the Fourier Transform of functions that have infinite energy. The first of these special functions is the Delta Function
![]()
Where Ge(t) is any function from the set of all functions having the properties
1.
![]()
2.
![]() For all t ¹ 0
For all t ¹ 0
Sifting Property of the Delta Function
Integrating the product of the Delta Function with a “well-behaved” function results in “sampling” the “well-behaved” function at the time that the Delta Function goes to infinity. Or

Proof
Use Integration by parts

Let U(t) = f(t) and dV(t) = d(t-t0)dt
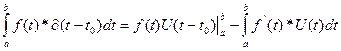
Case 1: a < t0 < b
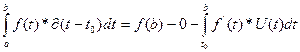

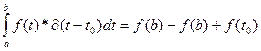
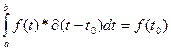 Q.E.D
Q.E.D
Case 2: t0 < a or t0 > b
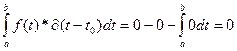 Q.E.D
Q.E.D
Example 2
Take the Fourier Transform of a constant
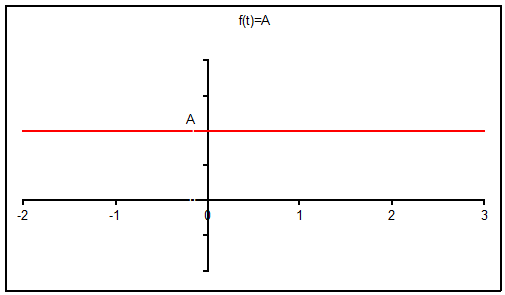
![]()
Here the integral can’t be directly computed, we have to approach it as a limiting case. Let’s replace the constant with a parameterized function that equals the constant as its parameter approaches zero, the double-sided exponential function:
![]()
Now the Transform becomes:

Let u = -w in the first integral
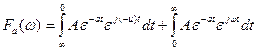
From our first example this is:
![]()
![]() Now we need to take the limit as
a 0 to get F(w)
Now we need to take the limit as
a 0 to get F(w)
![]()

so this is a d-function that goes to ¥ at w = 0 if its integral is a constant.
![]()
Let a*x = w
![]()
![]()
![]()
![]()
![]()
Therefore
![]()
Exercises:
1: Find the Fourier Transforms for each of the two pulses

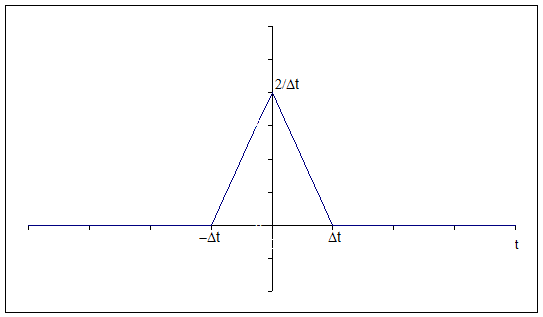
2: Find the transfer function for the simple RC low-pass filter
|
|
3: Determine the Fourier Transform of the RC low-pass filter output due to each of the pulses in part 1
![]() 4: Find the limit of each of the results
in part 3 as Dt 0
4: Find the limit of each of the results
in part 3 as Dt 0
Properties of the Fourier Transform
Symmetry Property
![]() If f(t) F(w)
If f(t) F(w)
![]() Then F(t) 2p f(-w)
Then F(t) 2p f(-w)
Proof:

Therefore
![]()
Let u = w and v = t
![]()
Now let w = v and t = u
![]()
![]() Therefore F(t) 2p f(-w)
Therefore F(t) 2p f(-w)
And if f(t) is an even function
![]() F(t) 2p f(w)
F(t) 2p f(w)
Linearity Property
![]() If f1(t)
F1(w)
If f1(t)
F1(w)
![]() And f2(t)
F2(w)
And f2(t)
F2(w)
![]() Then [a*f1(t) + b*f1(t)] [a*F1(w) +
b*F2(w)]
Then [a*f1(t) + b*f1(t)] [a*F1(w) +
b*F2(w)]
Proof:
Results due to the linearity of integration
Scaling Property
![]() If f(t) F(w)
If f(t) F(w)
Then for a real
![]() f(a*t)
f(a*t) ![]()
Proof:
![]()
case 1: a > 0 Let x = a*t
![]()
![]()
or
![]()
case 2: a < 0 Again let x = a*t
![]() (Note the
limits are now backwards)
(Note the
limits are now backwards)
![]()
or
![]()
Therefore including both cases
![]() f(a*t)
f(a*t) ![]()
Q. E. D.
Note: The compression of a function in the time domain results in an expansion in the frequency domain and vice versa.
Frequency Shifting
If ![]()
Then ![]()
Proof:
![]()
![]()
![]()
or
![]()
Q. E. D.
Note: The Modulation Theorem (very important in communications)
Remember Euler’s Identities
![]() and
and ![]()
therefore
![]()
or
![]()
similarly
![]()
or
![]()
Time Shifting
If ![]()
Then ![]()
Proof:
![]()
![]()
![]()
![]()
Q. E. D.
Time Differentiation and Integration
If ![]()
Then ![]()
And ![]()
Proof:
First for differentiation (part 1)
![]()
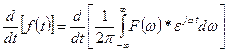
![]()
![]()
![]()
or
![]() Q.
E. D. for part 1
Q.
E. D. for part 1
Now for integration (part 2)
![]()
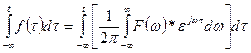
Interchanging the order of integration
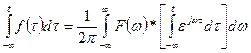
![]()
![]()
or
![]() Q. E. D. for
part 2
Q. E. D. for
part 2
Frequency Differentiation
If ![]()
Then ![]()
Proof:
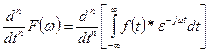
![]()
![]()
![]()
or
![]() Q. E. D.
Q. E. D.
The Convolution Theorem
Definition: the convolution of two functions ![]() is defined as:
is defined as:
![]()
Time Convolution
If ![]()
And ![]()
Then ![]()
Proof:
Therefore

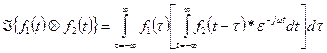
Let u = t - t in the inner integral

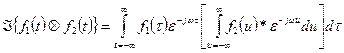
Since the inner integral is no longer a function of t, it can be brought out as a constant and this leaves
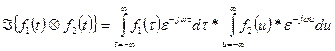
or
![]() Q. E. D
Q. E. D
Frequency Convolution
If ![]()
And ![]()
Then ![]()
Proof: Same method
as for time convolution