Generalized Fourier Series
Definitions
1.
0 Ai
(¹
0 or ¥)
if i = j
![]()
![]()
A set of functions {Fi(t)}
is said to be orthogonal over an
interval [a,b] iff
![]()
2. A set of functions is said to be complete over an interval [a,b] if any waveform with a finite number of discontinuities on [a,b] can be expressed as a linear combination of members of that set.
Theorem: The Fourier Series
Given: {Fi(t)} is a complete, orthogonal set on [a,b],
![]() , and
, and
f(t) has a finite number of
discontinuities on [a,b].
Then: ![]() over [a,b]
over [a,b]
Where: 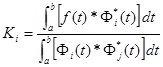
Proof:
Since {Fi(t)} is a complete set on [a,b]
![]() over
[a,b]
over
[a,b]
Multiplying both sides of the equation by ![]() yields
yields
![]()
Now integrating both sides over [a,b]
![]()
Reversing the order of integration and summation (linear operators) and moving the constants out of the integral leaves
![]()
But
![]() 0 for i ¹ j so
we are left with only the ith term of the
sum
0 for i ¹ j so
we are left with only the ith term of the
sum
![]()
Solving for Ki
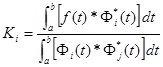
Q. E. D.
Examples of Complete, Orthogonal Sets
|
{Fi(t)} |
[a,b] |
|
{ 1, sin(nw0t), cos(nw0t) } ( 1 ³ n ³ ¥ ) |
[ -T/2, T/2] ( T = 2p/w0 ) |
|
{ exp(jnw0t) } ( - ¥ ³ n ³ ¥ ) |
[ -T/2, T/2] ( T = 2p/w0 ) |
|
Pn(t) – The Legendre Polynomials |
[ -1, 1 ] |
|
r0 = 2.41, r1 = 5.51, r2 = 8.64, r3 = 11.79, …
|
|
Example: The Sawtooth or Sweep function

f(t) = (A/T)*t
t in [0, T)
Use { 1, sin(nw0t), cos(nw0t) } (w0 = 2*p/T)
0 0
![]()

 First find a0
First find a0
![]()
note: the second and third integrals are zero since the area under a sine or cosine over a integer number of cycles is always zero. They have equal areas above and below the axis.
![]()
![]()
Solving for a0
![]()
![]()
a0 = A/2 Note: This is the average or
DC value of the waveform
Now
find bn for n ³
1
again
![]()
![]() Now multiply both sides by and integrate over
the interval
Now multiply both sides by and integrate over
the interval
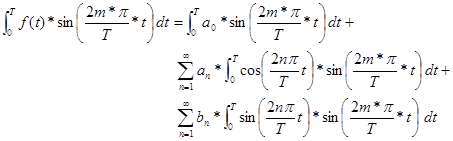
The first integral is zero as before; the second is also zero since
![]() HW: check it out
HW: check it out
The third integral uses another trigonometric identity
![]()
The (x+y) terms again all yield zero and all of the (x-y) terms are also zero except for the one where m=n. This yields
![]()
But cos(0) = 1 and the integral becomes T and we have
![]()
or
![]()
Integrating this requires the use of integration by parts
![]()
We want to get rid of the t in the integral so let u = t and dv be the rest. This yields
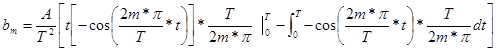
The integral is once again zero for the usual reason. The first term becomes
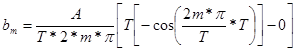
Simplifying further
![]()
or
![]()
HW: Show that the an are all zero for
n ¹ 0
The Complex Exponential Series: Another form of the Sine-Cosine Series
Euler’s Formula
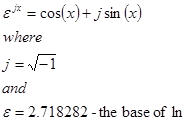
This also means that
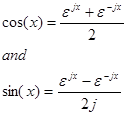
The unit circle represents exp(x) as a unit vector of magnitude 1 and angle q

sin(x) cos(x) 1
![]()
q
![]()
![]()
![]()
The complex exponential is therefore closely related to the Phasor analysis used in AC circuits and
![]()
HW: find the complex exponential form for the Fourier Series of the sawtooth example function.
Note: the answer should be consistent with
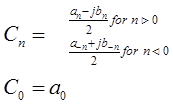
Note: Both the Sine-Cosine and Complex Exponential sets consist of members that are periodic functions. Each of their members has a frequency, which is a multiple of the fundamental frequency that has a period, T, equal to the length of the region of orthogonality. Each element is also periodic with period T and therefore their sum is also periodic.
Although we made no general statement in the theory about the behavior of the original function outside of the region of orthogonality, the Fourier series will only represent a periodic function. It, however, will represent a periodic function over all time.
Further note: at discontinuities, there will be some residual error
