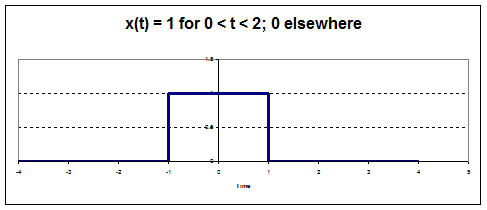
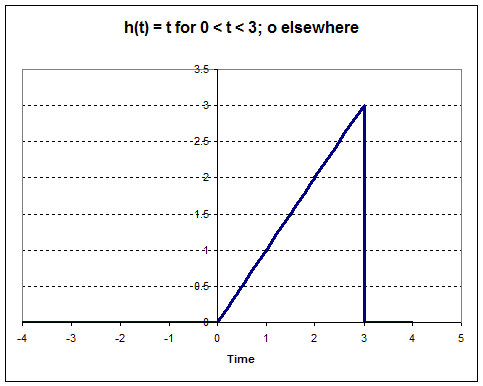
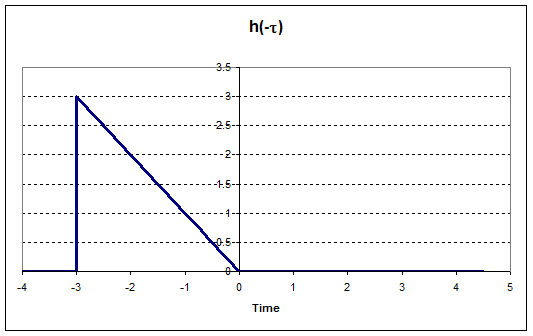
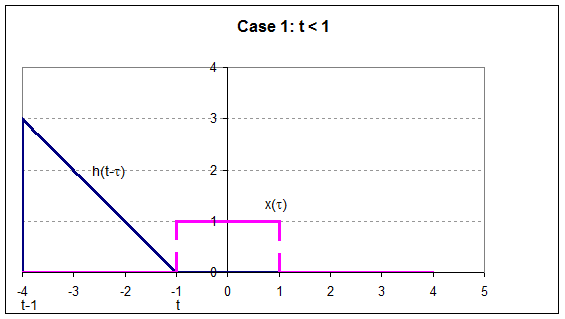
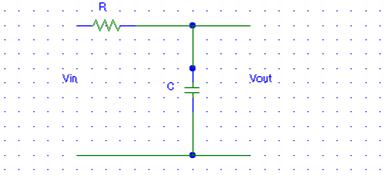
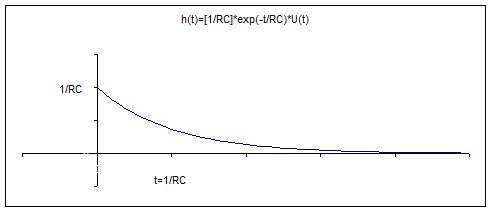
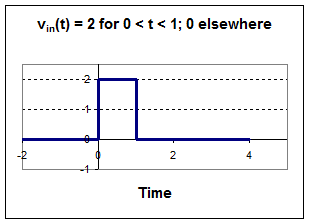
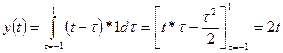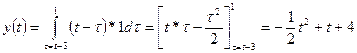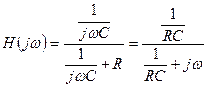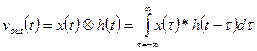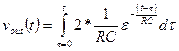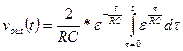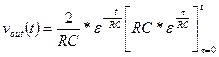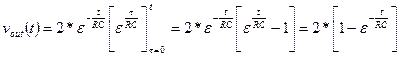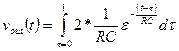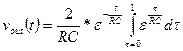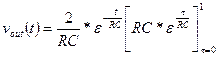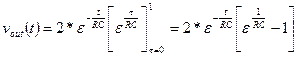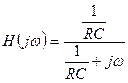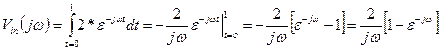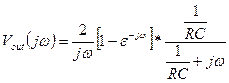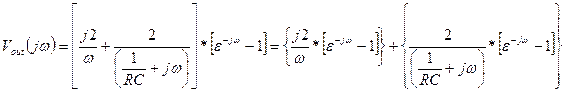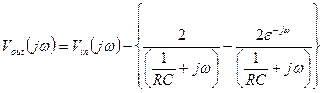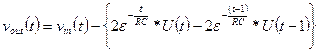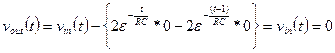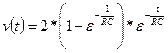Linear Time-Invariant Systems (LTI)
Introduction
This section introduces the analysis of Causal, Linear, Time-invariant, Continuous systems.
- Causality: The system response depends only on inputs in the past. Excitations that will occur in the future can have no effect on the present output.
- Linearity: Superposition applies to these systems.
![]()
![]()
![]() If
x1(t) y1(t)
If
x1(t) y1(t)
and x2(t) y2(t)
Then a* x1(t) + b* x2(t) a* y1(t) + b* y2(t)
Nonlinear systems are common in the real world. You will run into them in your studies of Communication Systems and Digital Signal Processing. Don’t try to apply the methods described here on non-linear systems, as they will NOT work.
- Time Invariance: These systems will behave the same now as they did yesterday. The phase of the moon has no effect. Time varying systems are also common, but we will assume an unchanging world here.
- Continuous: All variables are defined along the real line (or in the complex plane). Time progresses forward in a smooth continuous manner. System behavior can be completely described by a set of differential equations.
The input-output relationship of an LTI system can be defined in one of several ways
- Time-Domain Microscopic view: This was the first approach you used to analyze physical systems. The system behavior is described at each instant of time in terms of a set of Differential Equations and a present State.
- Time-Domain Macroscopic view: Here the system is modeled as having memory. The system output is produced as a weighted sum (integral) of its past inputs. The weighting function is called the system Impulse Response and the output is the Convolution of the past input with the Impulse response.
- Frequency Domain view: In the section on Fourier Signal Analysis the concept of the frequency domain was introduced. Now we can use the System Transfer Function to describe how the system processes the frequency domain representation of the input signal to produce the frequency domain representation of the output signal. Note that a closely related approach based on the Complex Frequency Domain (s-Domain) is covered in the section on LaPlace Transform Analysis. Both approaches are equally valid. Fourier is heavily used in Communications, while LaPlace is preferred for Feedback Controls and, in a discrete-time formulation (the Z-Transform), for Digital Signal Processing.

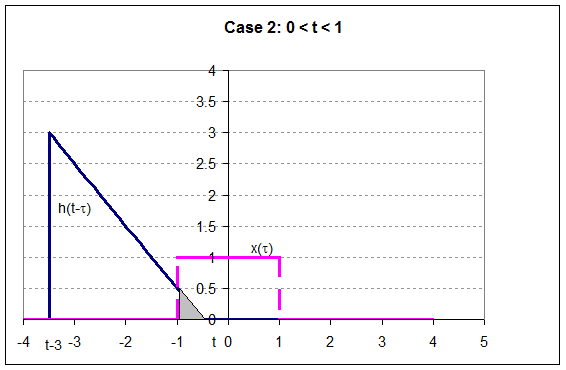
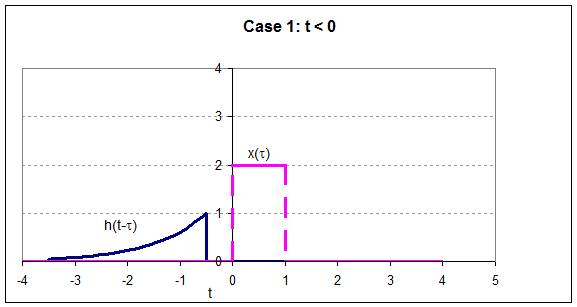
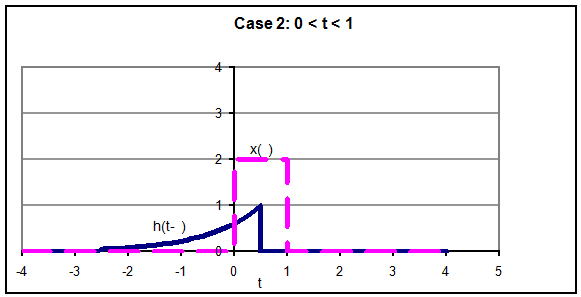
The Convolution Integral
Assume that the input, x(t), to an LTI system started at time t0 (the
input was zero for all time prior to t0) and has continued to the
present time, t, as shown below.
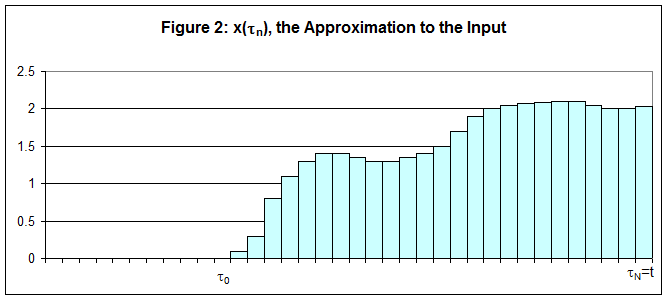
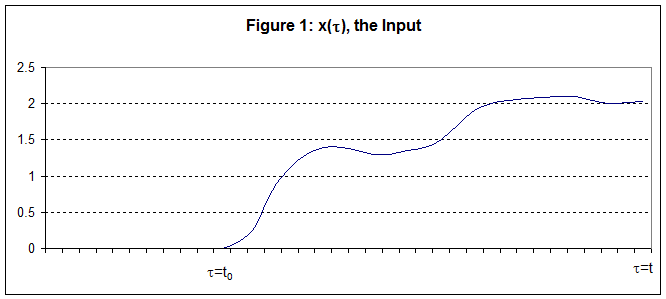
We can approximate this input as a series of
rectangular pulses having the same area under the curve as shown in Figure 2.
These graphs are given in
terms of the variable t, the variable t is reserved for the time of observation of the output
signal. The interval from t = t0 to t = t is divided into
subintervals of width Dt each centered about an value of tn = t0 + n*Dt.
Now perform the following
experiment. Apply a rectangular pulse of
unit strength and width Dt to the input of our LTI system. Lets call the resulting output f(t, tn).
- f(t, tn) is
the output at time t due to a rectangular pulse of unit amplitude and
width Dt that occurred at time t = tn .
The output of the system at
time t due to the nth pulse of the approximate input is then the
value of the input at time tn ,which
is x(tn), times f(t, tn). Using superposition the total output from the
system at time t is then approximated by the sum:
![]()
Multiplying and dividing each
term in the sum by Dt yields:
![]()
![]() Note
that the term
Note
that the term ![]() is the output of the time t due to a pulse of amplitude
is the output of the time t due to a pulse of amplitude ![]() that occurred at time t = tn . The area of
this input pulse ise equal to unity. Our
approximation gets better as Dt approaches zero so take the limit of y(t) as Dt 0 changing the sum to an
integral.
that occurred at time t = tn . The area of
this input pulse ise equal to unity. Our
approximation gets better as Dt approaches zero so take the limit of y(t) as Dt 0 changing the sum to an
integral.
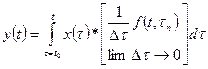
The term in the brackets
becomes the output at time, t, of the system to d(t-t), a Dirac Delta function or impulse that occurred at time t . It is usually denoted as h(t, t), or since our system is
time invariant simply h(t-t). This function, h(t), is
called the Unit Impulse Response of the system (which happens to
be the Inverse Fourier Transform of the Transfer Function, H(jw) ). The output
then is given by:
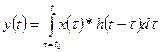
or, where it is up to you to
determine the limits on the integral from the nature of the two functions:
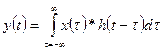
This is known as the Convolution
Integral and is denoted as:
![]()
Note: The meaning of Convolution is that an
LTI system can be modeled as having a memory that stores all past input. Acording to this model, the LTI system
determines its output by performing a weighted sum of all past inputs using the
Impulse Response as the weighting factor.
Continuous
systems seldom actually function this way, but this model accurately determines
the output. Many Discrete-Time
LTI systems ARE built according to the Convolution
model. They are called Finite Impulse
Response systems since their memory has a limited capacity.
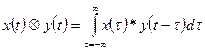
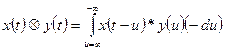
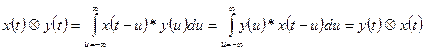
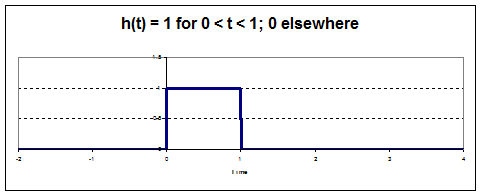
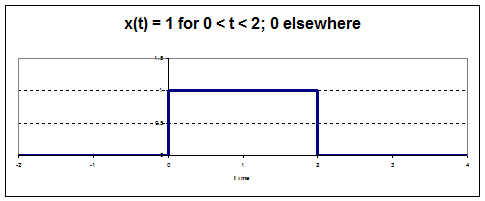
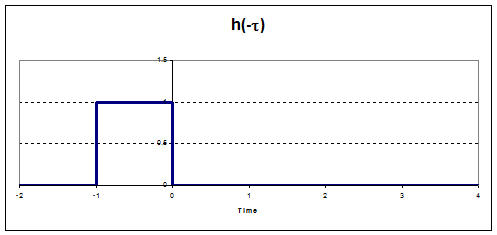
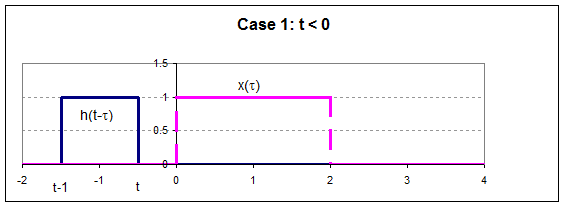
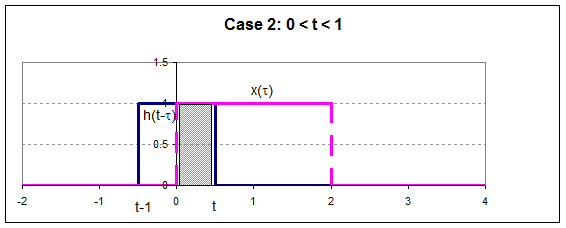
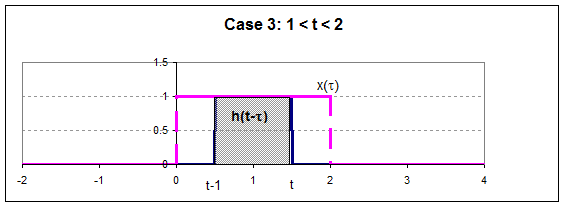
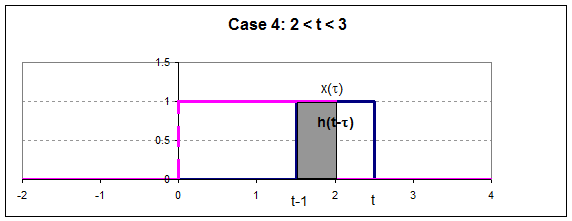
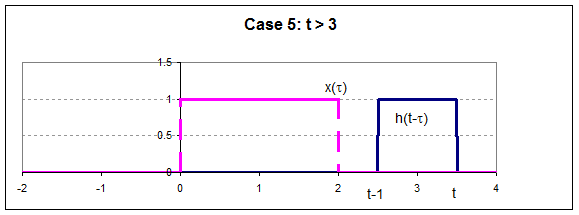
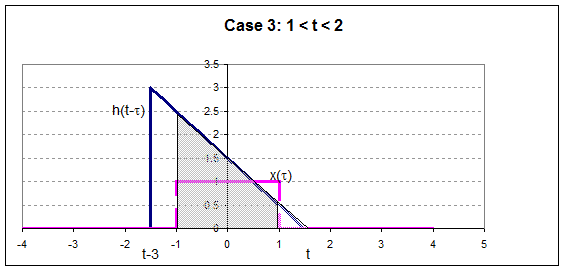
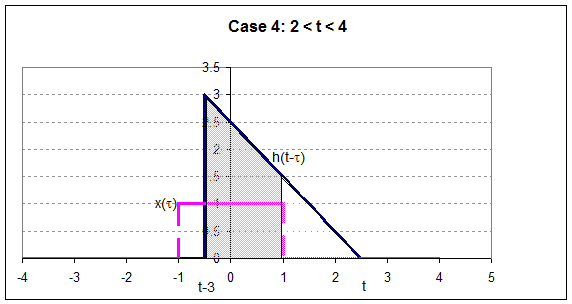
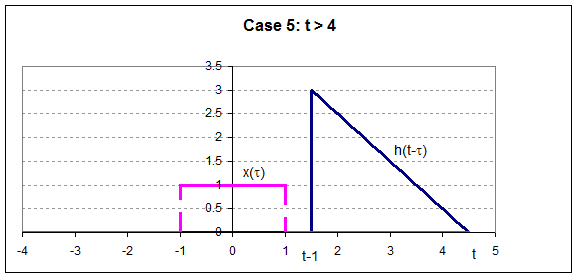
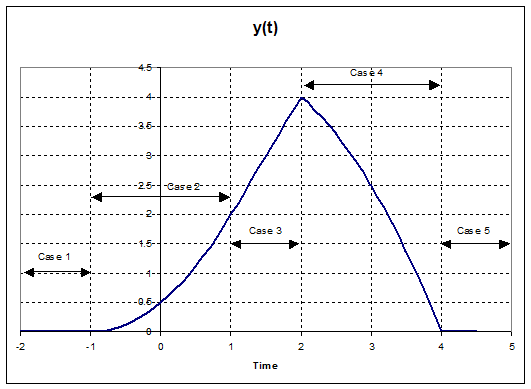
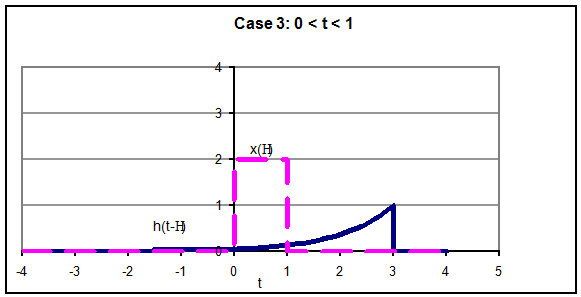
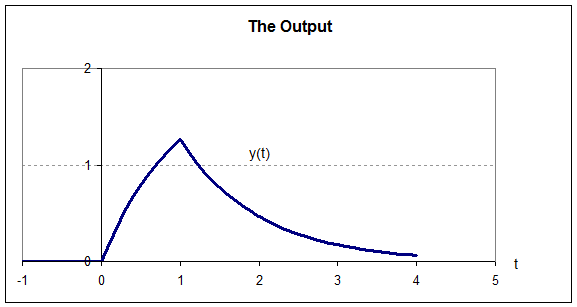
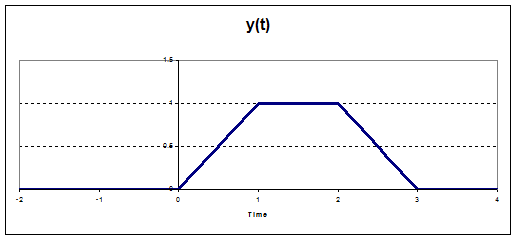 So
now we can plot the output,
So
now we can plot the output,