We need to calculate either:
1 - ( P(0) + P(1) ) or,
sum up all other cases.
P(0) = 0.85 = 10-5*215 = 0.32
P(1) = 5*0.2*0.84 = 0.41 Note: 5 is the number of ways only one station can be broadcasting.
So the result we want is: 1 - 0.73 = 0.27
P(all correct) = 0.810 ~ 0.1
Therefore the average number of attempts is 1/P ~ 10
lambda = 1/arrival time = 1/10ms = 100 frames/s
u = 1.544 * 106 bps / (1500 B * 8b / B) = 128.7/s
a = lambda/u = .78
p = (1-a)aN / (1-a(N+1))
.05 = (1-.78) * .78N / (1 - .78(N+1) )
if N = 7 then .05 = (.22 ) * .18 / ( 1 - .14)
Therefore we need to hold 7 packets which is 7 * 1500 = 10500 bytes.
Reference: The Finite Buffer Case from Vastola's "Probability and Queuing" (RPI).
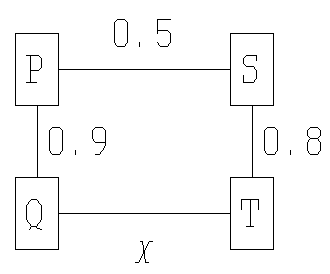 In the diagram below, the numbers
represent line reliability expressed as the
probability of each line remaining intact during bad
weather. To preserve (direct or indirect)
communication among all nodes, no more than 1 line
may break. If the probability of communication among
all nodes must be no less than 72% during bad
weather, what is the minimum reliability required of
line QT?
In the diagram below, the numbers
represent line reliability expressed as the
probability of each line remaining intact during bad
weather. To preserve (direct or indirect)
communication among all nodes, no more than 1 line
may break. If the probability of communication among
all nodes must be no less than 72% during bad
weather, what is the minimum reliability required of
line QT?
P = P(none bad) + (P one bad)
.72 = 0.5*0.8*0.9*X + 0.5*0.8*0.9*(1-X) + 0.5*0.8*(1-0.9)*X + 0.5*(1-0.8)*0.9*X + (1-0.5)*0.8*0.9*X
.72 = 0.36X + .36 - 0.36X + 0.04X + 0.09X + 0.36X
0.72 = 0.36+0.49X
X = 0.36/0.49 = 0.735
Therefore, the reliability of X must be better than 0.735