A Property of CRC Generator Polynomials
How do we know that generator polynomial G(x) = x3+1 can detect all 2-bit errors in adjacent bits?
Let T'(x) = T(x)+E(x), be the incorrectly received message created by adding the original message T(x) to an error polynomial E(x). To represent a 2-bit error in a pair of adjacent bits, error polynomial E(x) must have the form xi+1+xi, which factors into xi(x+1).
To pass undetected, the expression T'(x)/G(x) must give remainder 0. This expression is a sum of two terms:
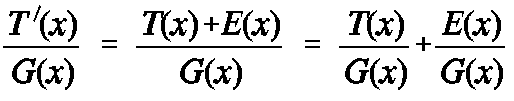
The first term is T(x)/G(x). By definition of polynomial T(x), it leaves remainder 0 when divided by G(x). Therefore expression T'(x)/G(x) has remainder 0 if and only if E(x)/G(x) has remainder 0. In other words, to pass undetected, G(x) must evenly divide E(x), leaving remainder 0.
Does G(x)=x3+1 evenly divide E(x)=xi(x+1), leaving remainder 0? The first factor, xi, is a power of x and is therefore not divisible by x3+1. Furthermore, they have no common factors. The second factor, x+1, has degree less than G(x) and is therefore also not divisible by x3+1. Thus, E(x)/G(x) has a non-zero remainder, and therefore so does T'(x)/G(x). Therefore, all errors in a pair of adjacent bits, are detected.
It turns out that any E(x) error polynomial of degree less than G(x)'s is detectable when G(x) has 1 as its last term.
This is because all such error polynomials factor into the form xi(xr-1+
... +1) where r is the degree of G(x). The first factor,
xi, is a power of x, and is therefore not
divisible by any G(x) having a term 1, nor do they have any common
factors. The second factor, xr-1+ ... +1, has degree less
than G(x), and is therefore also not divisible by G(x). Thus,
all the following standard generator polynomials have the form xr+
... +1:
CRC-12
x12+x11+x3+x2+x+1
CRC-16
x16+x15+x2+1
CRC-CCITT
x16+x12+x5+1
Having 1 as the last term of G(x) also helps detection of error bursts, E(x), with degree equal to or greater than G(x)'s. This is because a burst can only pass undetected, when all r bits of the remainder of E(x)/G(x) are 0. According to the definition of a burst, the first and last bits of E(x) are defined to be 1, while the last bit of G(x) is chosen to be 1. The next-to-last r bits of E(x)/G(x)'s remainder have 50% chance of matching, assuming that the error altered them randomly. Only when all r bits match does the burst escape detection, and this event has probability ½r.
In the special case when E(x) has degree exactly r, then because its first bit is defined to be 1, as well as its last bit, divisor G(x) matches in both first and last bit positions. This leaves only r-1 other bits unknown. This case therefore escapes detection with probability ½r-1.
The Shift-Register Implementation of CRC Polynomial Division
The modulo-2 polynomial division used for CRC Polynomials is conveniently implemented using a shift register of r bits, where r is the degree of the CRC polynomial. The following C fragment illustrates such an implementation:
BOOLEAN morebits(void);
BIT nextbit(void);
BITREGISTER shiftreg, crc;
while (morebits())
{
if (FIRSTBIT(shiftreg) == 1) shiftreg ^= crc;
shiftreg= (shiftreg << 1) | nextbit();
}
In the fragment above, the input shifts left (operator <<) 1
bit at a time. When a 1 appears in the first bit of the shift register the
post-CRC-division remainder is determined (exclusive-or operator ^=) for all
bits in parallel, at each step of the division.
The corresponding hardware shift register depends on a circuit which has a shift register stage for the low order r bits of the CRC polynomial. Each stage which represents a 1 polynomial coefficient is preceded by an exclusive-or gate. The exclusive-or gates are connected to sense the first shift register bit. This corresponds to the first bit of the dividend. When the first bit is 0, the shift register shifts each bit into the stage to its left. However, when the first bit is 1, bits which pass through an exclusive-or gate are inverted as they are shifted. This determines the post-CRC-division remainder for all bits in parallel, at each step of the division.
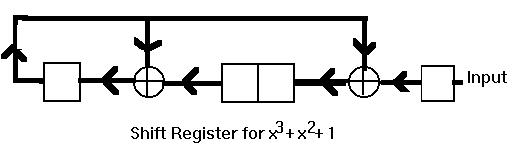
In both software and hardware, after the message polynomial has passed through the input, the shift register contains the remainder which should be 0 for a correctly received message. This remainder can be shifted out of the first shift register bit by shifting r 0 bits into the input.