|
ABSTRACT
While
the use of sinusoidal electromagnetic waves as information carriers is
taken as one of the principal axioms of today's wireless system design,
certain nonsinusoidal waves may further enrich the scope and capacity
of modern wireless engineering. Two notable nonsinusoid examples are
impulses and chaotic signals. The short temporal width of impulses has
enabled applications such as ranging radars and ultra wideband (UWB).
The complex nature of chaotic signals offers a new means of encrypted
communication. Here we review a new circuit paradigm, the electrical
soliton oscillator, which can self-generate both impulse and chaotic
signals of very large bandwidth by leveraging the singular dynamics of
a nonlinear wave known as the electrical soliton. By combining a
nonlinear transmission line with a unique amplifier that can "tame" the
inherently unruly dynamics of solitons, the oscillator self-generates a
stable, periodic train of short impulses. If the taming functions of
the amplifier are turned off, the circuit self-generates chaotic
signals by positively exploiting solitons' unruly nature. While still
in its early stages, this soliton circuit may one day serve as the
heartbeat of both impulse and chaotic wireless systems.

Introduction: Impulse and Chaotic Communications, and Electrical Solitons
Information transmission using a radio-frequency sinusoidal signal is a
well-established and enormously fruitful paradigm in modern wireless
technology. In spite of this hegemony that will undoubtedly last into
the foreseeable future, there also have long been efforts and some
remarkable successes in utilizing wideband nonsinusoids as
information-bearing signals. The rationale for these unorthodox efforts
lies in that the physical properties of certain nonsinusoidal signals,
most notably impulses (short baseband pulses) and chaotic signals, can provide certain advantages over the sinusoidal signal.
An example of a wireless system that uses impulses is the impulse ranging radar [1]. Its operating principle is diagrammed in Fig. 1a.
A locally generated impulse is sent over a delay line and out into free
space. The impulse transmitted into the free space hits an object and
is reflected. The reflected pulse is received and propagated on the
delay line where the portion of the locally generated impulse was
already traveling. The position on the line where the received pulse
meets the locally generated impulse can be detected and translated into
ranging of the object. A shorter width of the impulse directly
corresponds to a higher ranging resolution: one picosecond pulse width
corresponds to a ranging resolution of 0.3 mm. In addition to this
radar-specific high-accuracy ranging advantage, impulses offer benefits
in the general communication context, including large bandwidth,
immunity to multipath fading, good penetrating capability, and low
probability of detection, all of which are more pronounced with shorter
impulse duration. With such advantages over their sinusoid
counterparts, impulse wireless systems have been steadily developed
over the past 40 years. Their future pervasiveness may be debated, but
impulse radars and radios are likely to share some of the mainstream
communication market for certain applications in the booming
ultra-wideband (UWB) revolution.1
The use of a chaotic signal for information transmission is an extreme
example of nonsinusoidal signal use. The theory is to utilize chaotic synchronization
[2] to "privately" synchronize a transmitter and a receiver. Just as
two coupled sinusoidal oscillators can be frequency-synched via
injection locking, two coupled chaotic oscillators can synchronize
their chaotic outputs, converging from distant initial conditions [2].2 Shown in Fig. 1b, a chaotic transmitter generates a chaotic carrier signal c(t) and the transmitter sends out a modulated version c(t) + m(t), where m(t)
is the information signal. An identical chaotic oscillator acts as a
receiver, and coupled with the transmitter's oscillator by a common
signal, produces a synchronized replica of c(t). The information m(t) is recovered as the difference between the receiver's input c(t) + m(t) and the synchronized replica of c(t).
The commercial viability of this curious technology conceived in 1990s
(e.g., [3, 4]) still remains to be seen. However, due to its potential
for secure communication as an alternative to or an enhancement of
conventional software-based and quantum-cryptographic systems, it is
drawing significant attention from research communities, producing
proof-of-concepts in circuits and laser systems [3, 4].
Furthering of the two highly interesting technologies, impulse and
chaotic communications, or assessing how far they will reach in the
future, would require studies from all spheres of communication
engineering. This article is especially concerned with the circuit
aspect, and reviews the electrical soliton oscillator
recently developed by the authors [5, 6] (see also [7] for a review).
This unique circuit self-generates a periodic train of short impulses
or, alternatively, a chaotic signal, the essential commodities of
impulse and chaotic communications,3
and thus crosses the two poles of spectrum, order and chaos.
Utilization of peculiar — and fascinating — nonlinear wave pulses known
as solitons [8] in the electrical domain lies at the heart of the
circuit. Soliton pulses are by nature unruly. By promoting the unruly
behaviors, the chaotic soliton oscillator is attained. By "taming" the
unruly behaviors, the stable soliton oscillator that self-generates the
periodic train of electrical soliton impulses is obtained.
Circuits capable of impulse and chaotic signal generations [3] already
abound, so why bother with the electrical soliton oscillator? The
distinctive engineering advantage of electrical soliton pulses lies in
their extremely short pulse duration, which can be made as small as one
picosecond [9, 10]. The stable soliton oscillator can potentially
generate a periodic train of these ultra-short soliton pulses, and the
short pulse duration will maximize all of the aforementioned benefits
of impulse communications (e.g., bandwidth, ranging resolution, etc.).
Similarly, the chaotic signal produced by the chaotic soliton
oscillator can potentially have a bandwidth as large as one terahertz
due to the extremely short soliton pulse. This directly corresponds to
an increased data rate in chaotic communication.
The two following sections review the history of solitons and their
hallmark properties so as to provide a background. The rest of the
article describes the electrical soliton oscillator in both stable and
chaotic regimes. Now before diving into the business of electrical
solitons, we would like to emphasize that applications mentioned in
this article, especially chaotic communication, are in the embryonic
stages, and are discussed here only to propose a possible opportunity.
Solitons: A Brief Chronicle
Solitons are highly localized pulse-shape traveling waves that are
found in nonlinear dispersive media. They maintain spatial localization
of wave energy in a pulse in the course of propagation (no dispersion)
and exhibit singular nonlinear properties. In the absence of loss,
solitons propagate perfectly preserving their shape. The soliton
phenomenon is caused when nonlinearity counteracts dispersion. Soliton
history is as intriguing as its phenomenon, warranting a brief
description.
Just like the legends told about Newton's apple and Archimedes'
"Eureka!" moments, it was by serendipity that the Scottish naval
engineer Scott Russell first discovered solitons in shallow water in
Edinburgh's Union Canal in 1834. As he watched a barge being pulled
along the canal by horses, the rope connecting the barge to the horses
suddenly snapped. The mono-pulse "solitary" water wave created by the
prow's rapid dip into the water traveled quickly down the canal with
unnoticeable change in shape over several kilometers, which Russell
observed by following the wave on horseback. The unusually low
dispersion and long preservation of shape of the wave so provoked
Russell that he built a water tank in his garden for follow-up studies.
Not only did his experiments reproduce the solitary wave of low
dispersion, but it also revealed other unique properties of the wave.
There ensued intellectual efforts to understand Russell's experiments.
A majority of authorities, including Stokes, eventually disputed
Russell's work, but Rayleigh argued in support of Russell. No firm
conclusion was drawn and discussion was out in the open. Then, in 1895
came an unappreciated breakthrough when Korteweg and DeVries derived a
nonlinear wave equation that modeled the shallow water wave, including
both nonlinearity and dispersion. They solved this now-celebrated "KdV"
equation to attain a traveling-wave solution of permanent shape,
matching Russell's experiments. Unfortunately, KdV's triumph went
largely unnoticed for more than half a century. It was not realized
that in addition to being the governing equation of the solitary wave
in shallow water, the KdV equation can describe solitary waves in a
variety of physical systems (e.g., plasma, crystal lattice). People
also did not understand the underlying mechanisms of the KdV solitary
wave beyond what Russell phenomenologically observed.
The general significance, fundamental physical mechanisms, and
far-reaching implications of the KdV solitary wave were finally fully
uncovered by Zabusky and Kruskal in 1965 [11]. By analyzing their
computer experiments with the KdV equation to study plasma and
nonlinear crystals, they rediscovered the KdV solitary wave, which they
explained is made possible by balance between nonlinearity and
dispersion. Zabusky and Kruskal further found that when two solitary
wave pulses collide, they interact strongly but then emerge thereafter
recovering their original shapes as if there had been no interaction at
all (only a phase shift occurs as a consequence). To emphasize this
particle-like nature of solitary waves, they coined the name solitons (like photon, electron, etc.).
Zabusky and Kruskal's work marks the beginning of an intense surge of
research activities in solitary waves from various disciplines in
science and engineering, and the importance of solitons has only
increased. Solitons are now taken as an emblem of nonlinear phenomena.
KdV solitons as well as solitons described by other types of equations
are now known not only in shallow water, crystals, and plasma, but also
in magnetically ordered media, Bose–Einstein condensates, and
technologically important optical fibers in the form of light-wave
solitons. Another technologically interesting soliton is the electrical
soliton, as it can be utilized in electronics that touches our everyday
life. Now let us turn our attention to electrical solitons.
Electrical Solitons: A Primer
In the electrical domain, the nonlinear transmission line (NLTL) serves
as a nonlinear dispersive medium and, as such, can create electrical
solitons. The NLTL has been extensively used during the past 40 years
for sharp soliton pulse generations [9, 10]. The NLTL (Fig. 2a)
is constructed from a normal transmission line (two conductors running
in parallel) by periodically loading it with variable capacitors
(varactors), such as reverse-biased pn junction diodes, whose
capacitance changes with applied voltage. Alternatively, the NLTL can
be obtained by forming an artificial ladder network of inductors and
varactors (Fig. 2b).
The nonlinearity of the NLTL originates from the varactors since their
capacitance varies with applied voltage. The dispersion of the NLTL
arises from the structural periodicity of the NLTL (periodic lumped
varactor loading).
For certain pulse-shaped voltage waves on the NLTL, the nonlinearity
balances out the dispersion, and they propagate maintaining their shape
in the absence of loss. These are electrical solitons, and are
described by the KdV equation. The general wave solution on the NLTL
obtained by solving the KdV equation is a periodic train of soliton
pulses, also known as a cnoidal wave (Fig. 2c). For a given NLTL, an infinite number of cnoidal waves are possible via different combinations of the amplitude V0, pulse spacing 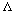 , and pulse width W. Initial or boundary conditions will determine a specific cnoidal wave that can propagate. Figure 2d
shows the special mono-pulse electrical soliton, whose cousin in
shallow water was observed by Russell. When loss is present solitons
cannot maintain their shape, but they still maintain spatial
localization of energy in a pulse shape through a unique damping
process [5]. , and pulse width W. Initial or boundary conditions will determine a specific cnoidal wave that can propagate. Figure 2d
shows the special mono-pulse electrical soliton, whose cousin in
shallow water was observed by Russell. When loss is present solitons
cannot maintain their shape, but they still maintain spatial
localization of energy in a pulse shape through a unique damping
process [5].
Let us now look at some other relevant — and beautiful — properties of
electrical solitons (or any KdV soliton) as a necessary background to
understand the soliton oscillator. To begin with, a taller soliton
travels faster than a shorter one. Due to this amplitude-dependent
speed, if a taller soliton is placed behind a shorter one (Fig. 2e, top), the taller one will catch up with the shorter one and move ahead of it after a collision (Fig. 2e). During the collision (Fig. 2e,
middle), the two solitons interact very strongly and experience a
significant amplitude modulation (nonlinear collision). After the
collision (Fig. 2e,
bottom), the two solitons return to their original shapes, but they
acquire a permanent time (phase) shift shown by the difference in d1 and d2 in Fig. 2e. Due to these properties, that is,
- Amplitude-dependent speed
- Amplitude modulation during the collision
- Phase modulation after the collision,
electrical solitons exhibit unruly behaviors in
an oscillator, as shown below. Promotion of these behaviors leads to a
chaotic soliton oscillator. Taming of the unruly solitons is necessary
to attain a stable soliton oscillator that self-generates a periodic
train of soliton pulses.
Nonsoliton waves can also propagate on the NLTL, but only by changing
their shape to form into a soliton or solitons. A nonsoliton input
close to soliton shape will be sharpened into a soliton (Fig. 2f,
top). A nonsoliton input significantly different from soliton shape
will break up into multiple solitons of different amplitudes (Fig. 2f,
bottom). In either case, the input pulse becomes compressed traveling
down the line. Once a soliton or solitons are formed, they propagate
without further sharpening or breakup. The past 40 years have seen this
transient electrical soliton-forming process occupying an especially
significant place in modern electronics for sharp pulse generation [9,
10], with the record pulse width of down to one picosecond [10]. This
unsurpassed electrical pulse width and correspondingly large bandwidth
make the soliton use for impulse and chaotic communications
significantly advantageous.
Self-Generation of
Electrical Solitons
In almost any wireless transceiver, one finds a dynamic circuit block
that incessantly signals a sinusoid — an electrical oscillator. The
oscillator is the heartbeat of wireless systems, providing frequency
references amongst transmitters and receivers. A popular form of the
sinusoidal oscillator consists of an EM resonator (e.g., LC
tank) and an amplifier [12]. The resonator shapes its output into a
sinusoid. The amplifier injects energy into the resonator to match
energy loss. The result is autonomy. While there is no sinusoidal
signal driving the oscillator and the only energy source is a dc power
supply, the oscillator self-generates a sinusoidal signal, initially
self-starting by amplifying ambient noise.
The stable electrical soliton oscillator we recently developed [5,6] is
the result of our original quest to build an analogue of the sinusoidal
oscillator. By combining a specially designed noninverting amplifier and a ring NLTL (Fig. 3a),
the circuit self-generates a periodic train of electrical soliton
pulses in steady state, initially self-starting from background noise.
The periodic soliton train corresponds to one of the soliton
circulation modes (Fig. 3b)
that can form on the ring NLTL, thus satisfying the boundary condition
that the ring's circumference should be an integer multiple of the
spacing between two adjacent solitons. The amplifier is special, since
in addition to providing gain to initiate a startup and to compensate
loss in steady state, it executes functions to "tame" the inherently
unruly behaviors of solitons, which we discussed above. If these taming
functions are removed from the amplifier, the solitons' unruly
behaviors are promoted, and the resulting oscillations are plagued with
instability problems, exhibiting chaotic behaviors with significant
variations in pulse amplitude and repetition. This chaotic oscillator,
however, can be positively exploited for chaotic communication.
The development of the electrical soliton oscillator marks a
distinctive and meaningful departure from the past 40 years' work on
the NLTL, which has been almost exclusively focused on generation of
electrical solitons by driving the NLTL with an external high-frequency
signal, as explained above via Fig. 2f (recreated in Fig. 3c).
In constrast, the electrical soliton oscillator is self-contained, not
requiring the external high-frequency input. In its stable operation
regime, the electrical soliton oscillator also provides a better
pulse-quality control than the traditional approach due to
self-regulatory mechanism inherent in any stable oscillator. The
electrical soliton oscillator is a newborn electrical cousin of soliton
modelocked lasers that have already proliferated in the optical domain
[13]. The rest of this article describes the detailed operation and
prototype results of the electrical soliton oscillator, in both the
chaotic and stable operation regimes.
Chaotic Electrical
Soliton Oscillator
Let us consider a case where a standard voltage-limiting noninverting amplifier is used in the soliton oscillator of Fig. 3a. The transfer function of the amplifier is depicted in Fig. 4a.
The amplifier is biased at a fixed operating point. Simulations show
that the soliton oscillator exhibits an unstable oscillation with
significant pulse amplitude and repetition rate variations (Fig. 4b).
The combination of the signal saturation in the amplifier and the
inherent properties of solitons described above causes this oscillation
instability. To see this, let us assume a soliton pulse appearing at
the input of the amplifier at a certain time (VX in Fig. 4c).
This soliton will turn into a square pulse after passing through the
amplifier, as the amplifier clips the top off of the input soliton (VY in Fig. 4c).
This square pulse will break up into multiple solitons of different
amplitudes traveling down the NLTL, as explained above (the rightmost
waveform in Fig. 4c).
The multiple solitons will travel at different speeds due to their
amplitude-dependent speed, eventually appearing again at the amplifier
input at different times. This process repeats, creating many solitons
with various amplitudes. These solitons circulate in the loop at
different speeds, continually colliding with one another. As discussed
above, these soliton collision events lead to phase and amplitude
modulations, rendering the oscillation unstable as in Fig. 4b.
Proving if the unstable oscillation is indeed chaotic is not
straightforward; it demands mathematical rigors. We instead take a
power spectral density of the oscillator output to observe the degree
of the spread of the signal power in the frequency domain, as is done
frequently [14]. A distribution of signal power over a broad range of
frequencies is a key signature of a chaotic signal, even though it is
not a sufficient condition for being chaotic. In our case, this method
would do as it has been already mathematically proven that a simple
NLTL with even three varactors can behave chaotically [8].
Figure 4d and Fig. 4e
are the simulated power spectral densities of the unstable oscillation
signals, for weaker and stronger nonlinearities of the NLTL,
respectively. A larger nonlinearity is obtained by making the voltage
dependence of the varactor capacitance more pronounced. With the weaker
nonlinearity (Fig. 4d), the power spectral density is concentrated over a finite number of certain frequencies. As the nonlinearity increases (Fig. 4e), the power spectral density is significantly broadened, strongly indicating a chaotic signal generation.
There already exist various chaotic circuits, (e.g., Chua's circuit, or
analog Lorenz chaos generator [3]). The distinctive advantage of the
chaotic soliton oscillator over the existing chaotic circuits lies in
its potential for an extremely large bandwidth. Due to the unique
ability of the NLTL to compress soliton widths down to one picosecond
or less, as demonstrated in [10] with an NLTL with Shottky diode
varactors in a GaAs technology, the chaotic soliton oscillator could
potentially generate a chaotic signal with a bandwidth approaching one
terahertz, and hence can be an excellent candidate for broadband
private chaotic communication.
Stable Electrical
Soliton Oscillator
While the chaotic soliton oscillator is a useful by-product that can be
positively exploited for broadband chaotic communication, in order to
attain a self-generated periodic train of stable soliton pulses for
impulse communication, oscillation instability needs to be suppressed.
The discussion in relation to Fig. 4
indicates that signal distortion has a negative impact on the
oscillation stability, suggesting that one might be able to obtain a
stable soliton oscillation if signal distortion is mitigated. We tried
a linear amplifier in the soliton oscillator of Fig. 3a,
which was able to produce a periodic soliton pulse train [5]. In the
same system, however, other oscillations uncontrollably appeared with
slight changes in gain, termination, or pretty much with any external
or internal perturbations, indicating a lack of robustness. These
waveforms sometimes contained multiple solitons with varying
amplitudes/spacings and pulses continuously moved relative to one
another and collided, yielding what looks like Fig. 4b
again. This experiment suggests that distortion reduction is a
necessary, but not a sufficient condition to stabilize the oscillation.
In addition to the signal distortion in the amplifier, there are two
other instability sources that need to be removed. First, in
steady-state oscillation, any small ambient perturbations such as noise
should be attenuated, which otherwise could grow into parasitic
solitons. Unless the perturbations are attenuated, the desired soliton
circulation mode and parasitic solitons will propagate at different
speeds due to their generally different amplitudes, colliding to cause
phase and amplitude modulations, hence building up oscillation
instabilities. Second, only one soliton-circulation mode should be
selected in steady state among many possible modes of Fig. 3b.
If this is not achieved, various modes with generally different
amplitudes will circulate in the loop at different speeds, leading to
soliton collision events and unstable oscillations.
The identification of these stability mechanisms, that is,
- Distortion reduction
- Perturbation rejection
- Single mode selection,
was an important initial step for our electrical
soliton oscillator development [5, 6]. We subsequently implemented
these stability mechanisms in a standard saturating amplifier by
incorporating an adaptive bias control. Note that the transfer curve of
the saturating amplifier is just like the one in Fig. 4a that caused chaotic oscillation, but the difference lies in the adaptive bias control. With Fig. 5, we will explain how the adaptive bias control works and how it achieves the three stability mechanisms.
Figure 5a
shows the transfer curve of the amplifier, which is divided into the
attenuation, gain, and saturation regions, based on the curve's
tangential slopes. At startup, the amplifier is biased at A in
the gain region so that ambient noise can be amplified to kick off
oscillations. As the oscillations grow and form into a pulse train, the
dc component of the amplifier output increases (Fig. 5b). This increase in the dc component is used to adaptively lower the amplifier bias (dashed arrow in Fig. 5a).
The reduced bias corresponds to an overall gain reduction, since a
portion of the pulse enters the attenuation region as the bias moves
down the curve. The bias continues to move down until the decreasing
overall gain eventually becomes equal to the system loss, settling at
the steady-state bias B (Fig. 5a).
In steady state with the bias at B,
the three stability requirements are simultaneously met. First, the
reduced bias ensures that the peak portions of the input pulses do not
enter the saturation region, reducing distortion. Second, with the
reduced bias, the steady-state input soliton train is placed across the
attenuation and gain regions, causing small perturbations around the
bias to be attenuated. Note that perturbation rejection is accomplished
while maintaining gain for main portions of input soliton pulses to
compensate loss. This threshold-dependent gain-attenuation mechanism is
a technique widely employed in modelocked lasers (lasers that generate
a train of periodic light pulses) in optics, where it is known as saturable absorption.
Interestingly, this technique was originally introduced in electronics
domain by Cutler for his liner pulse oscillator [15]. Third, the
dependence of the steady-state bias on the dc component of the
amplifier output leads to a mode-dependent gain since each mode has a
different dc component. This naturally leads to a single-mode
selection, for which details can be found in [5].
Note that to achieve distortion reduction (first stability mechanism),
the top portion of the amplifier nonlinearity in the transfer curve,
the boundary between the gain and saturation regions, is avoided, while
to achieve perturbation rejection (second stability mechanism) while
maintaining gain, the bottom portion of the amplifier nonlinearity in
the transfer curve, the boundary between the gain and attenuation
regions, is exploited.
The adaptive bias-control amplifier concept is general, and can be implemented in a variety of forms. Figure 5c
shows an example oscillator implementation [5, 6] with the amplifier
inside the dashed box. The amplifier consists of two inverting stages:
one built around an nMOS transistor, M1, and the other built around a
pMOS transistor, M2. Together they form a noninverting network. The
adaptive bias control is implemented for both stages. It functions as
follows for the pMOS stage. The output waveform VY sensed by the Ra-Rb voltage divider is integrated by the R2-C2 low-pass filter. The integrated voltage V2 represents a scaled dc component of VY. Now V2 is fed back to the gate of M2 to set its bias. As the dc level of VY increases, V2
will rise with respect to ground, which corresponds to a reduction in
the gate-source voltage of M2, effectively lowering its bias. A similar
scenario applies to the nMOS stage. Combining the two stages, the bias
of the amplifier at the input is reduced as the dc component of VY increases, thus performing the adaptive bias control.
Three additional points are noteworthy. First, although the adaptive bias control in Fig. 5
uses the signal's dc component, it can be alternatively executed by
using the signal's peak to expedite start-up transients. Second, the
termination of Fig. 5
is needed to absorb energy. This termination cannot be perfect because
NLTL's characteristic impedance is voltage-dependent. However, the
resulting small reflections are attenuated by the amplifier's
perturbation rejection mechanism, the second stability mechanism.
Third, one can implement simple switches to activate and deactivate the
bias-feedback network to toggle between the stable and chaotic
oscillation regimes.
Three prototypes confirmed the concept of electrical soliton oscillator [5, 6]. The first two prototypes (Fig. 6a and Fig. 6b) were built using discrete components to explicitly examine detailed dynamics of the soliton oscillator. The third prototype (Fig. 6c)
was implemented on a CMOS IC to demonstrate a chip-scale operation.
Each prototype self-generated a periodic train of solitons pulses.
The lowest frequency prototype (Fig. 6a) allows for a detailed view of the oscillation startup (Fig. 6d).
The oscillator self-starts by creating a small oscillation, eventually
growing into a steady-state soliton pulse train. During this process,
another completing mode is clearly seen (red): it first grows with
time, but is eventually suppressed by the stabilizing mechanism of the
amplifier. One can also see the shorter pulse (competing mode, red-)
propagate at a different speed than the taller pulse (main mode that
survives, black): in this time-domain measurement at a fixed point on
the NLTL, the shorter pulse originally behind the taller pulse catches
up with the taller pulse and eventually moves ahead of it after
collision. In the space domain, this corresponds to the taller pulse
propagating faster than the shorter pulse, a key signature of solitons.
For other fascinating dynamics of the soliton oscillator, readers are
referred to [5].
Further Design Considerations
Our work so far has been focused on the demonstration of the stable and
chaotic soliton oscillator concepts, the former with confirming
experimental results and the latter with simulations. The minimum pulse
width of 293 ps in our latest stable soliton oscillator prototype (Fig. 6c)
is not a record number, but the prototypes were intentionally made
relatively slow in order to explicitly examine signals in a real-time
oscilloscope.
Now with the electrical soliton oscillator concept firmly demonstrated,
the oscillator, in either stable or chaotic operation regime, can be
quickly extended to a significantly higher speed. This can be done by,
for instance, integrating ultrafast GaAs NLTLs [10], which were shown
to produce picosecond soliton pulses, in our electrical soliton
oscillator. The utilization of such ultrafast NLTLs is expected to
increase the signal bandwidth up to one terahertz in the chaotic
soliton oscillator, and to decrease a pulse width down to one
picosecond (and increase pulse repetition rate up to about forty
gigahertz) in the stable soliton oscillator.
Placing such an ultrafast NLTL in the electrical soliton oscillator
raises an important question about the impact of the amplifier
bandwidth on the minimum soliton pulse width. While the propagation of
a 1-ps-wide pulse on an NLTL is feasible as demonstrated in [10],
amplifiers, even in the state-of-the-art solid-state technologies,
cannot provide bandwidth for such a sharp pulse. The experimental
studies in [5] clearly suggest, however, that the soliton compression
on the NLTL may be able to overcome the bandwidth limitation of the
amplifier, and hence, it may be feasible to achieve a 1 ps pulse width
using the NLTL despite the relatively slower amplifier. The explicit
demonstration of this interesting possibility remains an open question,
and would be a natural future extension of this work.
Finally, in addition to the bandwidth, power consumption, and area,
there are also important design considerations. The chip-scale stable
soliton oscillator shown in Fig. 6c occupies an area of about 3  7 mm and consumes dc power of about 20 mW. The relatively large area is
due to the use of bonding wires as the NLTL inductors, but the size can
be significantly reduced by using an on-chip NLTL and operating at
higher speeds. How the dc power consumption would scale with the speed
remains to be studied. The original soliton oscillator topology shown
in Fig. 3a
uses lumped voltage amplification, and is not energy efficient. A
distributed soliton oscillator where power gain is distributed all
along the NLTL could enhance the energy efficiency as well as the
speed.
7 mm and consumes dc power of about 20 mW. The relatively large area is
due to the use of bonding wires as the NLTL inductors, but the size can
be significantly reduced by using an on-chip NLTL and operating at
higher speeds. How the dc power consumption would scale with the speed
remains to be studied. The original soliton oscillator topology shown
in Fig. 3a
uses lumped voltage amplification, and is not energy efficient. A
distributed soliton oscillator where power gain is distributed all
along the NLTL could enhance the energy efficiency as well as the
speed.
Conclusion
While a sinusoidal signaling of information is a powerful paradigm that
communication engineers have matured over nearly a century, the past
decades have also seen possibilities in communications using
nonsinusoidal signals such as impulses and chaotic signals. If they
prove useful in real-world communication, the electrical soliton
oscillator may serve as the heartbeat of these unorthodox communication
systems. The electrical soliton's superb capability of pulse width
compression and resulting large bandwidth give an edge to the
electrical soliton oscillator over other impulse and chaotic signal
generation circuits. This prospect is brightened by the fact that
nature's most intricate and brilliant communication network, the human
brain, utilizes soliton-like neuron impulses and, often, their chaotic
behaviors.
References
[1] G. F. Ross, U.S. patent 3,728,632, Apr. 17, 1973.
[2] L. M. Pecora and T. L. Carroll, "Synchronization in Chaotic Systems," Physical Rev. Lett., vol. 64, no. 8, Feb. 1990, pp. 821–25.
[3] K. M. Cuomo and A. V. Oppenheim, "Synchronization of Lorenz-based Chaotic Circuits with Applications to Communications," IEEE Trans. Circuits and Sys. II, vol. 40, no. 10, Oct. 1993, pp. 626–33.
[4] R. Roy and K. S. Thornburg Jr., "Experimental Synchronization of Chaotic Lasers," Physical Rev. Lett., vol. 72, no. 13, Mar. 1994, pp. 2009–15.
[5] D. S. Ricketts, X. Li, and D. Ham, "Electrical Soliton Oscillator," IEEE Trans. Microwave Theory and Techniques, vol. 54, no. 1, Jan. 2006, pp. 373–82.
[6] D. S. Ricketts and D. Ham, "A Chip-Scale Electrical Soliton Modelocked Oscillator," IEEE Int'l. Solid-State Circuits Conf. Dig. Tech. Papers, Feb. 2006, pp. 432–33.
[7] T. H. Lee, "Electrical Solitons Come of Age," Nature, vol. 440, Mar. 2006, pp. 36–37.
[8] M. Toda, Nonlinear Waves and Solitons, Kluwer, 1983.
[9] M. J. Rodwell et al., "Active and Nonlinear Wave Propagation Devices in Ultrafast Electronics and Optoelectronics," Proc. IEEE, vol. 82, no. 7, July 1994, pp. 1037–59.
[10] D. W. van der Weide, "Delta-Doped Schottky Diode Nonlinear Transmission Lines for 480-fs, 3.5-V transients," Applied Physics Lett., vol. 65, no. 7, Aug. 1994, pp. 881–83.
[11]
N. J. Zabusky and M. D. Kruskal, "Interactions of Solitons in a
Collisionless Plasma and the Recurrence of Initial States," Physical Rev. Lett., vol. 15, no. 6, 1965, pp. 240–43.
[12] W. Andress and D. Ham, "Standing Wave Oscillators Utilizing Wave-Adaptive Tapered Transmission Lines," IEEE J. Solid-State Circuits, vol. 40, no. 3, Mar. 2005.
[13] C. J. Chen, P. K. A. Wai, and C. R. Menyuk, "Soliton Fiber Ring Laser," Optics Lett., vol. 17, no. 6, Mar. 1992, pp. 417–19.
[14] M. Wu, B. A. Kalinikos, and C. E. Patton, Physical Rev. Lett., vol. 95, 2005, p. 237202.
[15] C. C. Cutler, "The Regenerative Pulse Generator," Proc. IRE, vol. 43, no. 2, Feb. 1955, pp. 140–48.
Biographies
DONHEE HAM is an
associate professor of electrical engineering in the Division of
Engineering and Applied Sciences at Harvard University, Cambridge,
Massachusetts. He received a B.S. degree in physics in 1996 from Seoul
National University, Korea, graduating with Presidential Honor atop the
Natural Science College, and a Ph.D. degree in electrical engineering
from California Institute of Technology (Caltech) in 2002, winning the
Charles Wilts Doctoral Thesis Prize for outstanding Ph.D. research in
electrical engineering. He was the recipient of the Caltech Li Ming
Scholarship and IBM Graduate Research Fellowship. He was also the
recipient of the 2003 IBM Faculty Partnership Award. He shared
Harvard's Hoopes prize (best senior thesis award) in 2003 with William
Andress. His work experiences also include the Laser Interferometer
Gravitational Wave Observatory (LIGO), Pasadena, California
(1997–1998), IBM T. J. Watson Research Center, New York (2000), IEEE
conference technical program committees including International
Solid-State Circuits Conference, and industry/government technical
advisory positions on subjects including future silicon and nonsilicon
electronics technologies in the post-50 nm era. His current research
focus is on nanoscale quantum-effect devices for gigahertz-to-terahertz
circuits, soliton and nonlinear wave electronics, and RF and microwave
integrated circuits (ICs). His research also examines biological
laboratories on an IC.
XIAOFENG LI
attended Tsinghua University, Beijing, China for undergraduate study in
1998. After two years, he transferred to Caltech, where he received a
B.S. degree in 2004. He is currently working toward a Ph.D. degree at
Harvard University. His main research interest lies in the design and
experimentation of gigahertz-to-terahertz ultrafast quantum circuits
using nanoscale devices, such as quantum dots, nanowires, and carbon
nanotubes. He was the recipient of a Gold Medal at the 29th
International Physics Olympiad, Reykjavik, Iceland, 1998. He ranked
first in the Boston Area Undergraduate Physics Competition (U.S.
intercollegiate physics competition) in both 2001 and 2002. He was also
the recipient of the 2002 California Institute of Technology Henry Ford
II Scholar Award, the 2004 Harvard University Pierce Fellowship, and
the 2005 Analog Devices Outstanding Student Designer Award.
SCOTT DENENBERG
is in his senior year at Harvard University. He is expected to graduate
in the spring of 2007 with an S.B. in electrical engineering. He is
just beginning the process of applying to graduate programs in
electrical engineering, hoping to begin in the fall of 2007. This past
summer he joined Donhee Ham's group in researching the soliton damping
process in the stable soliton oscillator. He will be continuing his
work as part of a senior thesis project, looking into chaotic soliton
oscillators and their synchronizations. He has been on the Harvard
Men's Tennis team during his entire college career. He earned Varsity
letters in his sophomore and junior years, and was elected Captain of
the team at the beginning of his senior year. He and his doubles
partner were elected to the All-Ivy team at the end of their junior
year.
THOMAS H. LEE [M]
received S.B., S.M., and Sc.D. degrees in electrical engineering, all
from the Massachusetts Institute of Technology, Cambridge, in 1983,
1985, and 1990, respectively. In 1990 he joined Analog Devices, where
he was primarily engaged in the design of high-speed clock recovery
devices. In 1992 he joined Rambus Inc., Mountain View, California,
where he developed high-speed analog circuitry for 500 Mbyte/s CMOS
DRAMs. He has also contributed to the development of PLLs in the
StrongARM, Alpha, and AMD K6/K7/K8 microprocessors. Since 1994 he has
been a professor of electrical engineering at Stanford University,
California, where his research focus has been on gigahertz-speed
wireline and wireless integrated circuits built in conventional silicon
technologies, particularly CMOS. He has twice received the Best Paper
award at the International Solid-State Circuits Conference, co-authored
a Best Student Paper at ISSCC, was awarded the Best Paper prize at
CICC, and is a Packard Foundation Fellowship recipient. He is an IEEE
Distinguished Lecturer of both the Solid-State Circuits and Microwave
Societies. He holds 35 U.S. patents, and authored The Design of CMOS Radio-Frequency Integrated Circuits (now in its second edition) and Planar Microwave Engineering,
both with Cambridge University Press. He is a co-author of four
additional books on RF circuit design, and also cofounded Matrix
Semiconductor.
DAVID RICKETTS
received B.S. and M.S. degrees in electrical engineering from Worcester
Polytechnic Institute and a Ph.D. degree from Harvard University. He
worked in industry from 1995 to 2003 developing a wide array of analog
and mixed-signal integrated circuits in bipolar and submicron CMOS.
From 2003 to 2006 he was a research assistant at Harvard University,
where he developed soliton-based circuits and nanowire flexible
electronics. He joined the faculty of Carnegie Mellon University,
Pittsburgh, Pennsylvania, in 2006, where he is currently an assistant
professor of electrical and computer engineering. His research
interests include ultra-fast RF integrated circuits and devices,
soliton electronics, nanoscale electronics, and quantum devices. He was
awarded the Analog Devices Fellowship at Worcester Polytechnic
Institute, was a 2004 Innovation Fellow at Harvard University, and was
awarded the Analog Devices Outstanding Student Designer Award in 2006.
|