Continuous- Time Systems

A SYSTEM is an operation for which cause-and-effect relations exist.

Properties of Continuous- Time Systems

Here, we discuss some of the properties that a continuous-time system could have. We will use x(t) for the input to the system, y(t) as its output, and use the notation:

y(t)  =  T[x(t)]

or

y(t)  =  S[x(t)]

or

x(t)   →   y(t)

Systems with memory

Systems whose output depend on values of the input other than just at the time of the output have memory.
A system y(t₀) has memory if its output at time t₀ depends on the input x(t) for t > t₀ or t < t₀, i.e. it depends on values of the input other than x(t₀).

Otherwise, the system is MEMORYLESS

Example of a memoryless system:

Resistor v(t₀) = R i(t₀); the voltage depends only on current at time t₀.

Example of System with Memory:

Capacitor

the voltage depends on past values of current so a capacitor has memory.

Ex. Does y(t)  =  x(t)  +  5 have memory?

Ex. Does z(t)  =  x(t + 5) have memory?

Ex. Does y(t)  =  (t + 5)x(t) have memory?

Ex. Does z(t)  =  [x(t + 5)]² have memory?

Ex. Does a(t)  =  x(5) have memory?

Ex. Does v(t)  =  x(2t) have memory?

Inverse of a System

A system is invertible if you can determine the input uniquely from the output, i.e. there is a one-to-one relationship between the input and output.

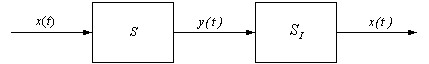
Resistor is Invertible, x(t) = i(t) , y(t) =  v(t), x(t) =  y(t)/R.

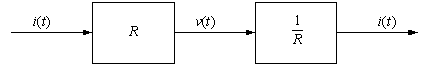
y(t) = x⁵(t) is an invertible system.

Noninvertible:

y(t) =  x(t)u(t)  →  zeros out much of the input
y(t) = x²(t) → don't know sign
y(t) =  cos[x(t)] → add 2π to x(t)

Causality

Output y(t) depends only on past and present inputs and not on the future.

All physical real-time systems are causal because we can not anticipate the future.

Image processing-Non-causal filters like blurring masks.

Music processing - record and process later - noncausal but not real-time

Ex. Resistor, Capacitor, and stock market are causal,

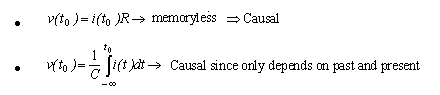
Non causal systems need off-line processing

Ex.

Is this Causal? You fill in.

FACT: Memoryless  →  Causal but not vice versa. In fact, most causal systems have memory.

Ex. Let y(t) =  x(-t).

Is this causal? Try letting t be a negative number.

Stability

Bounded Input - Bounded Output (BIBO) Stability

Input x(t) bounded produces bounded output.

If | x(t) |  B₁   →   | y(t) |  B₂, where y(t) is output.

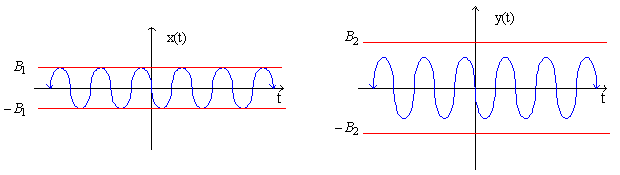
Example: Resistor is stable V=iR,

| i(t) |  B₁   →   | v(t) |  RB₁

Example:

Capacitor:

Is this stable?
Let i(t) = B₁u(t), where B₁≠0

grows linearly with t and as

,

. So capacitor is not BIBO stable.

Continue