We saw that I/O properties of LTI system are completely determined by system's impulse response h(t) and that the output y(t) = x(t) * h(t).
In this section, we will express other known system attributes in terms of conditions on h(t).
In a memoryless system, the output y(t) is a function of the input x(t) at time instant t alone.
An LTI system that is memoryless can only have this form:
y(t) = Kx(t)
K is the system gain and must be constant or else the system would vary with time.
y(t) = Kx(t) = x(t) * h(t)
For this to hold, h(t) must be of the form of an impulse weighted by K:
h(t) = Kδ(t)
What if
h(t) = Kδ(t - d), d ≠ 0?
y(t) = x(t) * h(t)
= Kx(t - d).
The time shift d implies memory.
y(t) depends on x(t - d), not x(t).
Example Is a system described by h(t) = u(t) - u(t - 1) memoryless?
h(t) * hI(t) = δ(t)
A system is invertible if we can find hI(t)
We will see how to do this when we study transforms.
We know that for a causal system, the output depends only on past or present inputs and not on future inputs.
Equivalently, a causal system does not respond to an input until it occurs (the output is not based on the future)
So, a response to an input at t = t0,
occurs only for t 
t0.
We know that h(t) is the system response to δ(t), and that δ(t) occurs at t = 0.
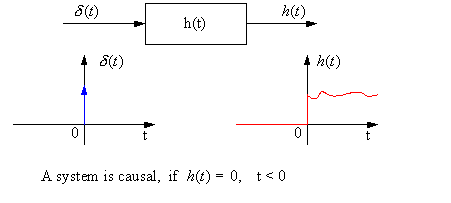
Examine convolution equation (flip h(t))
Causality: if h(t) is causal then h(t - τ) = 0, t - τ < 0 or t < τ.
So,
which shows us that the output y(t) depends only on values of
input x(τ) for
τ 
t.
Ex.
Is h1(t) = u(t + 1) causal?
Is h2(t) = u(t - 1) causal?
We can tell if an LTI system is BIBO stable from its impulse response.
Given a bounded input
|x(t)|
B1, for all t, check its output to see if it remains finite:
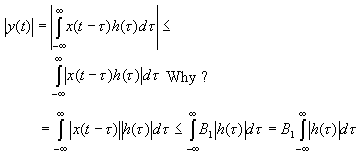
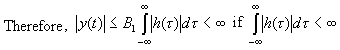
That is, if the impulse response h(t) is absolutely integrable:
Then,
|y(t)|
B2G = B2 and system is BIBO stable (sufficient
condition).
Ex. Is h(t) = u(t) stable?
running integral of x(t).
Ex. Given an impulse response h(t) = e-atu(t), a > 0, is the system BIBO stable? How about for a < 0?
running integral of h(t).
can find h(t) as derivative of s(t).
Ex. Given a step response
find the system's impulse response