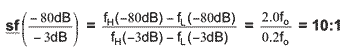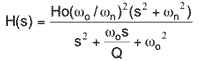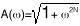|
 |
|
THE COMPANY
Frequency
Devices - founded in 1968 to provide electronic design engineers with
analog signal solutions and engineering services - today designs and
manufactures standard and custom signal conditioning, signal processing
and signal analysis solutions utilizing analog, digital and integrated
analog/digital technology. By addressing a wide array of signal
processing needs, Frequency Devices continues to provide
state-of-the-art solutions to the rapidly changing electronics
industry. From prototype to production, we design and manufacture
products to agreed-upon performance specifications, utilizing the
latest technologies. These module, subassembly and instrument hardware
and software solutions include analog and DSP (FIR and IIR) filters,
instrumentation grade amplifiers, low distortion signal sources and
data conversion products.
Focusing our talents on
precision performance while minimizing size allows us to offer our
customers some of the smallest, most precise, and cost-effective
signal-processing products available anywhere. By integrating our
superior technology into instrumentation products, we also provide
compact precision bench-top, laboratory and system solutions using
Compactpci, VME, VXI, and ISA architectures and RS232, IEEE-488, USB,
Ethernet or Firewire interfaces that permit high speed communication,
with high channel density in a minimum of space.
At
the heart of our solutions lie our analog and digital technologies.
Frequency Devices' ability to identify the design weaknesses of each
design approach and integrate their strengths to achieve a desired
performance objective through the use of layout techniques, packaging
skills and intellectual property results in analog, digital and mixed
signal solutions that provide superior performance. This superior
performance of Frequency Devices' solutions has earned the company a
place:
- On the international
space station where its active filter modules are used as anti-aliasing
filters in Boeing's Active Rack Isolation System (ARIS),
- At the LIGO observatory (a joint development
program affiliated with California Institute of Technology,
Massachusetts Institute of Technology and the National Science
Foundation), providing high resolution, low noise real-time data
processing digital-to-analog conversion that integrated precision
analog design with state-of-the-art 24-bit digital conversion,
- And on numerous OEM, R & D, and test
system applications in the health, space, defense, science,
engineering, and technology segments of the precision data acquisition
markets.
These applications
represent only a few examples of the myriad alternatives that Frequency
Devices offers to enhance the processing accuracy of analog, digital
and mixed-signal systems.
|
 |
|
|
|
Electronic Filter Design Guide
|
|
DIGITIZING SIGNALS AND ALIASING
Analog to Digital Conversion (A/D)
Most
physical (real world) signals are analog. Operating on these signals
efficiently often requires the filtering, sampling and digitizing of
the analog data using A/D converters. The converted digital data may
then be manipulated mathematically. Many data-acquisition systems must
also construct a representation of the original signal from the digital
data stream.
Unfortunately, sampling often
sacrifices accuracy for the sake of convenience. The digital version of
a signal may not resemble the original in some important respects. A
graphic example is the movie scene that apparently shows wagon wheels
or helicopter blades turning backwards. This erroneous image, known as
an "alias", occurs because a "motion picture" camera actually samples
continuous action into a series of stills, and the frame rate (commonly
24 or 30 frames per second) is not fast enough or is nearly an exact
multiple of the object's rotation speed.
According
to Nyquist's Theorem, accurately representing an analog signal with
samples requires that the original signal's highest frequency component
be less than the Nyquist frequency, which is at least half the sampling
frequency. To correct the image in the movie example, the frame rate
would have to exceed twice the rotation speed of the wheel (or its
spokes) or of the helicopter blades. No practical data-acquisition
system can sample fast enough to catch all of a real signal's
components. Frequencies above Nyquist appear as false low-frequency
aliases. As an example, Figure 1 shows the result of sampling a 900 Hz signal at 1 kHz.
|

Figure 1
 |
|
The
process seems to indicate that the original signal was a 100 Hz sine
wave, the difference between the actual input wave and sampling
frequencies. Note that as the maximum signal frequency approaches the
Nyquist frequency, the total number of samples needed to reconstruct
the signal accurately approaches infinity. Aliasing is a fundamental mathematical result of the
sampling process. It occurs independent of any physical sampling-system
capabilities. Downstream processing cannot reverse its effect. Only
filtering out the alias high frequency components before sampling
begins can prevent it.
When a signal undergoes
A/D conversion, the amplitude of any frequency component above Nyquist
should be no higher than the converter's least significant bit (LSB).
Some sources insist on reducing the amplitude to below half of the LSB.
For any full-scale undesirable signal component, then, attenuation
should be at least 6 dB x n, where "n" is the number of bits in the
A/D. For half of the LSB, attenuation would be 6 dB x (n + 1). A 12-bit
A/D, then, demands attenuation of 72 dB or 78 dB.
In
practice, noise-signal amplitudes rarely match the amplitudes of signal
components of interest, so this attenuation calculation represents
worst case.
IDEAL FILTER SHAPES (THEORETICAL)
Every
electronic design project produces signals that require filtering,
processing, or amplification, from simple gain to the most complex DSP.
The following presentation attempts to "de-mystify" some of these
signal-processing requirements. The concepts of ideal filters, commonly
used filter transfer function characteristics and implementation
techniques will assist the reader in determining their electronic
filter and signal conditioning needs.
Real-world
signals contain both wanted and unwanted information. Therefore, some
kind of filtering technique must separate the two before processing and
analysis can begin.
An ideal filter transmits
frequencies in its pass-band, unattenuated and without phase shift,
while not allowing any signal components in the stop-band to get
through. All filters offer a pass-band, a stop-band and a cutoff
frequency or corner frequency (fc) that defines the frequency boundary between the pass-band and the stop-band.
Figure 2
shows the four basic filter types: low-pass, high-pass, band-pass and
band-reject (notch) filters. The differences among these filter types
depend on the relationship between pass- and stop-bands.
|
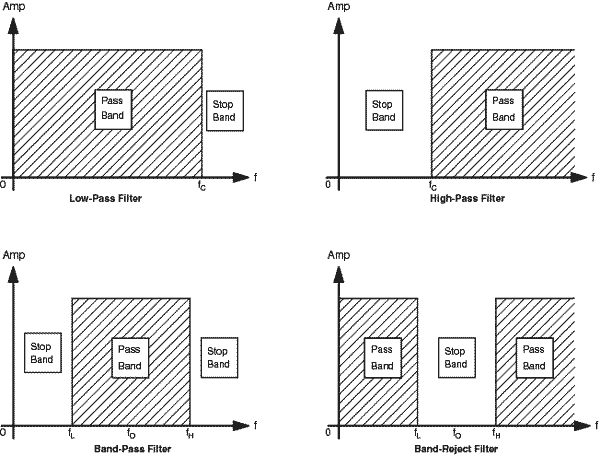
Figure 2
 |
|
Low-pass
filters are by far the most common filter type, earning wide popularity
in removing alias signals and for other aspects of data acquisition and
signal conversion. For a low-pass filter, the pass-band extends from DC
(0 Hz) to fc and the stop-band lies above fc .
In a high-pass filter, the pass-band lies above fc , while the stop-band resides below that point.
Combining high-pass and low-pass technologies permits constructing band-pass and band-reject filters. Band-pass filters transmit only those signal components within a band around a center frequency fo .An ideal band-pass filter would feature brick-wall transitions at fL and fH
, rejecting all signal frequencies outside that range. Band-pass filter
applications include situations that require extracting a specific
tone, such as a test tone, from adjacent tones or broadband noise.
Band-reject (sometimes called band-stop or notch ) filters transmit all signals except those between fH and fL
. These filters can remove a specific tone - such as a 50 or 60 Hz line
frequency pickup - from other signals. Another common application is
medical instrumentation, where high-impedance sensors pick up line
frequencies.
NON-IDEAL FILTERS (REAL WORLD)
Real-world
signals contain both wanted and unwanted information. Therefore, some
kind of filtering technique must separate the two before processing and
analysis can begin. Real filters are far from ideal. They subject input
signals to mathematical transfer functions with names like Butterworth,
Bessel, constant delay and elliptic that only approximate ideal
behavior. Instead of the sharply defined transition represented by
ideal filters, real filters contain a transition region between the
pass-band and the stop-band as shown in Figure 3.
|
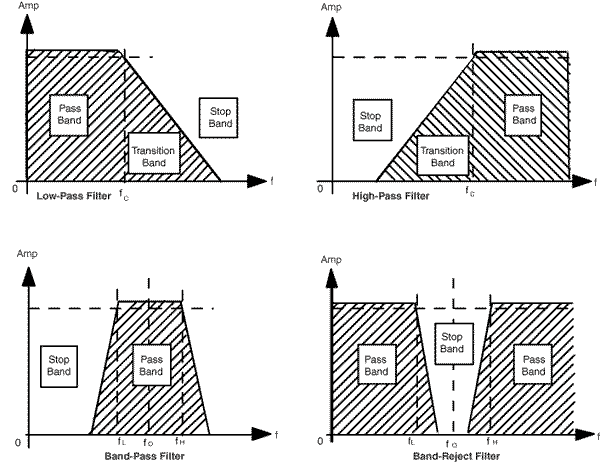
Figure 3
 |
|
In
addition, the pass-band is not flat like the ideal filter, may contain
attenuation ripple, and the attenuation in the stop-band may not be
infinite. In order to simplify the analysis of various real world
filter types, filter response curves are normalized. When selecting a
filter, this normalized data allows the designer to compare the
theoretical amplitude, phase and delay characteristics of each filter
type. Normalization
See Figure 4 below
for the theoretical performance characteristics and normalized response
curve of an 8-pole, 6-zero constant delay filter. The frequency axis on
the response plot is scaled so that the corner or ripple frequency is
always one Hertz instead of the actual intended corner or ripple
frequency. This allows one normalized curve to represent any filter
that would have the same response shape. To convert a normalized
amplitude response curve to a curve representing a filter whose corner
frequency is not at one Hertz, multiplying any number on the frequency
axis by the intended corner or ripple frequency scales the frequency
axis.
|
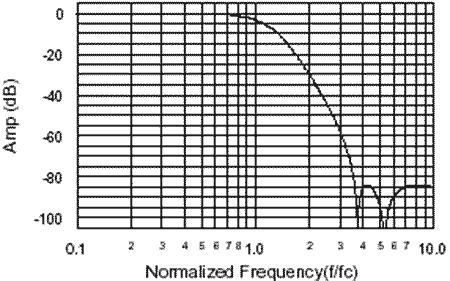
Figure 4 - Frequency Response
 |
|
Amplitude Response
Amplitude
Response is defined as the ratio of the output amplitude to the input
amplitude versus frequency and is usually plotted on a log/log scale as
shown in Figure 5. Note how the steepness of the transition band slope (roll-off) increases as the number of poles increase.
|
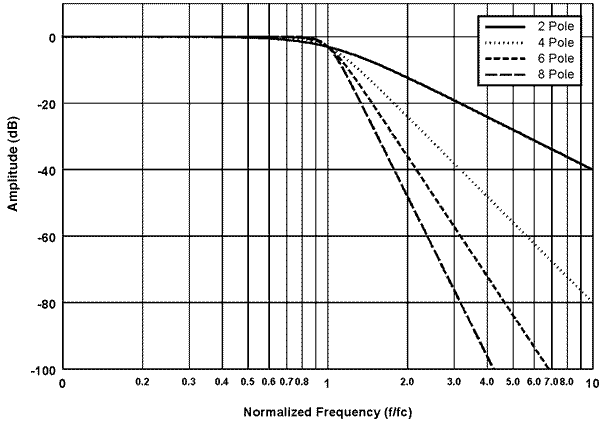
Figure 5 - 2, 4, 6, and 8 Pole Butterworth Lowpass
 |
|
Phase Response
All
non-ideal filters introduce a time delay between the filter input and
output terminals. This delay can be represented as a phase shift if a
sine wave is passed through the filter. The extent of phase shift
depends on the filter's transfer function. For most filter shapes, the
amount of phase shift changes with the input signal frequency. The
normal way of representing this change in phase is through the concept
of Group Delay, the derivative of the phase shift through the filter with respect to frequency.
| Group Delay (D) equation: |
D =
|
d
df
|
Group Delay
Group Delay is the phase slope on a linear phase vs. frequency plot. Figure 6 compares the group delay of some typical phase response curves.
|

Figure 6 - 8 Pole Lowpass, Group Delay Response
Butterworth, Bessel, Constant Delay, Elliptic
 |
|
Thus a point on a normalized group delay curve that has a group delay of one (1.0) second would yield 1 millisecond Actual Delay for a filter with a 1KHz corner frequency.
| Actual Delay = |
|
Normalized Group Delay
|
|
Actual Corner Frequency (fc) in Hz |
| Actual Delay = |
|
1.0 sec
|
= 0.001 sec/Hz |
|
1000 Hz |
Analog Filter Specifications
Low-Pass and High-Pass
In order to define the limits of the filter pass-band in real circuits, most filter specifications define the corner frequency (fc), as the frequency where attenuation reaches -3 dB or for elliptic filters, the ripple frequency (fr),
the point where the response curve last passes through the specified
pass-band ripple. Filter specifications may also include a shape factor
(sf) requirement, which describes how fast signals roll-off during
transition. The sf represents the ratio between the cutoff/ripple
frequency and where the filter achieves a desired attenuation level,
say (-80 dB).
Figure 7 is an elliptic filter that attenuates to -80 dB at 1.56 fr,
hence a shape factor of 1.56 to -80 dB. A high-pass filter with a 1.56
shape factor would achieve that same -80 dB of attenuation at fr/1.56 or 0.64 fr.
|
Filter Attenuation
|
|
(Theoretical) |
|
0.05 dB
|
|
1.00 fr
|
|
3.01 dB
|
|
1.05 fr
|
|
60.0 dB
|
|
1.45 fr
|
|
80.0 dB
|
|
1.56 fr
|
Also note that the elliptic transfer function attenuation floor is not infinite, but has notches and humps.
|
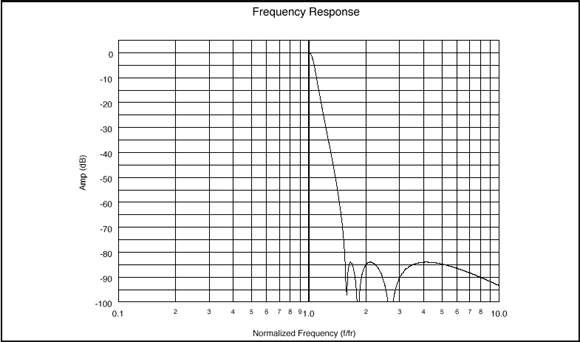
Figure 7
 |
|
From the attenuation table above, this low-pass elliptic filter has a -3 dB frequency of 1.05 at fr, therefore the shape factor is calculated as follows:
Band-Pass and Band Reject Filters
Specific items of interest for Band-Pass filters are the Center Frequency (geometric mean) fo, the Filter Bandwidth, the Quality Factor (Q) and the shape factor.
Frequency fo represents the geometric mean of fH and fL. That is:
fo = (fH * fL ) 1/2
Bandwidth is defined as the difference between pass-band extremes:
Bandwidth = fH - fL
The Quality Factor (Q) of a band-pass filter represents the ratio of the center frequency fo to the -3 dB bandwidth
Following is an example of band-pass filter calculations:
|
Filter
Attenuation
|
|
fH/fo
|
|
fL/fo
|
|
-3dB
|
|
1.105
|
|
0.905
|
|
-80dB
|
|
2.414
|
|
0.414
|
fH(-3dB) - fL(-3dB) = 1.105 fo - 0.905 fo = 0.20 fo
fH(-80dB) - fL(-80dB) = 2.41 fo - 0.414 fo = 2.0 fo
| Therefore: Q(-3dB) = |
|
fo
|
= |
fo
|
= |
5 |
|
fH(-3dB) - fL(-3dB) |
0.2 fo |
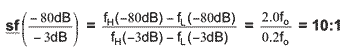
Figure 8
is a plot of a four pole-pair band-pass with a Butterworth transfer
function and a Q of 5. For band-pass filters, the shape factor shows
the ratio of the bandwidth at some attenuation level (say -80 dB) to
the specified pass-band bandwidth (the bandwidth at -3 dB). Its shape
factor at -80 dB is 10:1.
|
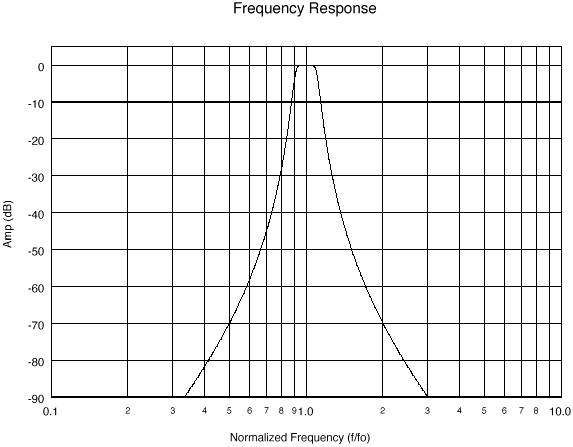
Figure 8
 |
|
A Band-Reject
filter's shape factor is the reciprocal of this number - that is, the
ratio of the pass-band bandwidth to the corresponding bandwidth at the
noted attenuation level. Filter Equations
Filter
transfer functions relate filter output to input through polynomials in
the Laplace-transform complex variable "S" as shown in Equation 1.
Using the "S" domain may seem confusing, but allows both the amplitude
and time response of a filter to be expressed in a simple format. A two
pole, two zero, low-pass filter can be expressed as:
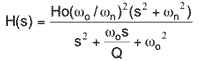
Equation 1
where: Ho = dc gain
Q = peaking factor at the corner frequency
 o = 2 o = 2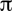 fo = filter corner frequency fo = filter corner frequency
 n = filter notch frequency n = filter notch frequency
Filters may include both Poles and Zeros. A Pole is any frequency that makes the denominator of the mathematical transfer function go to zero. A Zero
is a frequency that makes the transfer-function numerator go to zero.
Second-order transfer functions may contain two poles and up to two
zeros. To achieve steeper roll-off, higher-order real filters usually
include cascades of second-order and first-order filter stages.
To produce the phase and frequency response, "S" in the above equation is replaced by j  . Consider the second-order function that produces the amplitude versus frequency curve in Figure 9. . Consider the second-order function that produces the amplitude versus frequency curve in Figure 9.
|

Figure 9
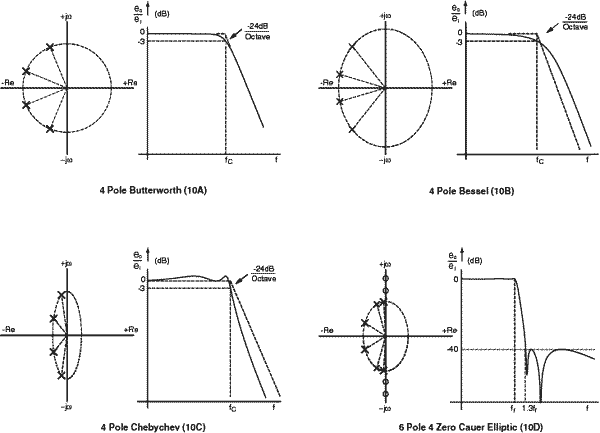
Figure 10
 |
|
Linear-active
filters can be made to closely match theoretical transfer functions.
Cascading first and second-order filter sections easily produces three,
four, five, six, seven, and eight-pole roll-off characteristics.
Performance is as good as the operational amplifiers that they contain.
With appropriate component selection, these filters contribute little
broad-band-noise and can achieve distortion levels lower than -100 dB.
Semiconductor switches permit corner-frequency programming without
significant noise, distortion, or other undesirable effects. These
filters are generally smaller than passive types for frequencies less
than 100 kHz. Filter-section corner frequencies - and therefore the
accuracy and shape of phase and amplitude curves - depend on amplifier
characteristics, passive-component accuracy and stability. ANALOG CIRCUIT DESIGN
Though there are several ways of constructing active filters, most applications use one of three topologies:
The Sallen-Key
topology injects signal into the non-inverting input of the opamp,
which is usually set for unity gain operation. This allows very
accurate unity gain in the filter passband. Distortion can be a problem
for the Sallen-Key design, as most opamps do not allow a large common
mode signal swing without adding distortion to the signal. Only one
opamp is needed to build a two-pole filter section.
The multiple feedback
topology also uses one opamp for a two pole section, injecting signal
into the inverting input of the opamp, usually with the non-inverting
input grounded. This limits common mode input voltage swing and
provides better distortion for larger signal swings. Gain set depends
on resistor ratios, so pass-band gain is dependent on the accuracy of
the resistors chosen. You can build high-pass filters in the multiple
feedback form though the input impedance decreases to a very low value
at higher frequencies. It is not possible to build multiple feedback
filters with zeros. Multiple feedback topologies are not as versatile
as other topologies.
For precision performance the state variable
topology is the hardest to design but provides the most versatility.
State variable designs require a minimum of three opamps and often are
realized using four opamps to increase the versatility even further.
Unlike the Sallen-Key and multiple feedback topologies, the state
variable filter Q, fo and pass-band gain can all be
independently set. This independence allows for higher precision
filters because of the reduced component tolerance buildup. The state
variable filter is the basis for most programmable filters.
An
active filter's amplifiers contribute DC offset, although careful
filter design can limit it to millivolt, and in many cases microvolt,
levels. This error is usually stable with time and changes little with
temperature. The amplifiers also add harmonic distortion to filter
output. However, since active filters can achieve distortion levels
less than -100 dB at frequencies up to 100 kHz and -110 dB at up to 20
kHz, they can easily pre-filter 16-bit (-96 dB) and 18-bit (-108 dB)
A/D converters.
FILTER SELECTION
Transfer functions can be classified into one of two basic categories, Amplitude filters and Phase filters.
Amplitude filters are designed for the best amplitude response for a
given situation, for example zero ripple in the amplitude response
pass-band. Phase filters are designed for desired phase response, such
as linear phase with frequency throughout the filter amplitude
pass-band.
Amplitude Filters
For
many applications the design goal is to approximate ideal "brick wall"
frequency response. Probably the most common amplitude filter transfer
function is the Butterworth, which consists of an array of poles uniformly distributed on a left-half-plane unit circle, as in Figure 10A. This arrangement yields the maximally flat amplitude response in the pass-band (the first 2n - 1
derivatives of the frequency response are equal to zero, where n is the
number of poles). Therefore, amplitude response rolls-off monotonically
(uniform slope) as frequency increases in the stop-band.
The attenuation ratio "A( )", of a Butterworth low-pass transfer function is given by: )", of a Butterworth low-pass transfer function is given by:
where N = degree of the filter (number of poles).
Butterworth
filters produce no pass-band ripple and provide theoretically infinite
attenuation as frequency increases when compared to fc . The primary limitation is, Butterworth filters produce slower roll-off than some of the alternative transfer functions.
The attenuation ratio of a Chebychev transfer function (Figure 6C) is given by:
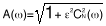
which generates a series of polynomials, where 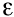 is pass-band ripple and CN is pass-band ripple and CN represents the nth order polynomial in the series. Table 1 shows the first five Chebychev polynomials. represents the nth order polynomial in the series. Table 1 shows the first five Chebychev polynomials.
Chebychev Polynomials CN
| N |
|
CN |
|
1
|
|
 |
|
2
|
|
2 2 - 1 2 - 1 |
|
3
|
|
4 3 - 3 3 - 3 |
|
4
|
|
8 4 - 8 4 - 8 2 + 1 2 + 1 |
|
5
|
|
16 5 - 20 5 - 20 3 + 5 3 + 5 |
Table 1
|
 |
|
 |
|
The
Chebychev function provides faster roll-off in the transition band than
a Butterworth filter would, but at the expense of some variation in the
pass-band called ripple. Ripple denotes that the amplitude in the pass-band varies between 1 and (1 + 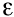 2), where 2), where 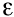 is always less than 1. Pole frequencies are more spread out and the Q's
of the sections are higher than the comparable section Q's of a
Butterworth. Determining pole locations involves applying hyperbolic
trigonometric functions to each pole of a Butterworth filter of the
same order. Like the Butterworth, Chebychev stop-band roll-off is
monotonic. It is important to note that many designers avoid Chebychev
transfer functions in favor of Cauer elliptic alternatives because
section Q's are higher for Chebychevs than with elliptic functions
which provide faster roll-off in the transition-band.
is always less than 1. Pole frequencies are more spread out and the Q's
of the sections are higher than the comparable section Q's of a
Butterworth. Determining pole locations involves applying hyperbolic
trigonometric functions to each pole of a Butterworth filter of the
same order. Like the Butterworth, Chebychev stop-band roll-off is
monotonic. It is important to note that many designers avoid Chebychev
transfer functions in favor of Cauer elliptic alternatives because
section Q's are higher for Chebychevs than with elliptic functions
which provide faster roll-off in the transition-band. Cauer elliptic transfer-function attenuation is given by:
where S = j  , ZN is the nth order elliptic polynomial, and , ZN is the nth order elliptic polynomial, and 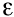 determines pass-band ripple attenuation at the cutoff frequency, determines pass-band ripple attenuation at the cutoff frequency,  = 1. Although an elliptic filter achieves faster roll-off than either
Butterworth or Chebychev varieties, it introduces ripple in both the
pass- and stop-bands. Also, elliptic filter roll-off is not monotonic,
eventually reaching an attenuation limit, called the stop-band floor.
= 1. Although an elliptic filter achieves faster roll-off than either
Butterworth or Chebychev varieties, it introduces ripple in both the
pass- and stop-bands. Also, elliptic filter roll-off is not monotonic,
eventually reaching an attenuation limit, called the stop-band floor.
For elliptic filters, shape factor depends not on the -3 dB corner frequency (fc), but on ripple frequency (fr),
the highest pass-band frequency on a low-pass filter or the lowest
pass-band frequency on a high-pass filter where pass-band ripple
occurs, as shown in Figure 11.
|
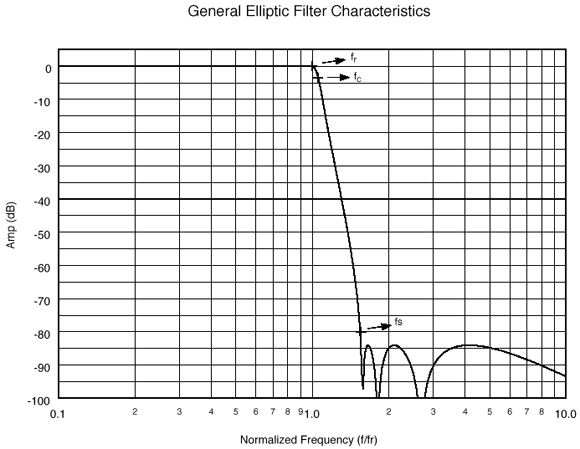
Figure 11
 |
|
At
the stop-band edge, a small frequency change produces a large change in
attenuation. Another critical element in the shape of an elliptic
filter is frequency fs, which denotes the first frequency at which the attenuation reaches the stop-band floor.
The pole configuration for this transfer function consists of a set of poles around an ellipse with pairs of zeros on the j axis, see Figure 10D.
Pole frequencies are spread out over the pass-band. Section Q's are
less than those in a comparable-order-and-ripple Chebychev. Desired
pass-band ripple, stop-band floor and shape factor determines actual
pole and zero locations in a particular filter. Figure 12
compares the amplitude response of eight-pole Butterworth, 0.1 dB
ripple Chebychev, and 0.1 dB ripple, -84 dB stop-band floor
Cauer-elliptic transfer functions. The curves are normalized to the -3
dB cutoff frequencies. axis, see Figure 10D.
Pole frequencies are spread out over the pass-band. Section Q's are
less than those in a comparable-order-and-ripple Chebychev. Desired
pass-band ripple, stop-band floor and shape factor determines actual
pole and zero locations in a particular filter. Figure 12
compares the amplitude response of eight-pole Butterworth, 0.1 dB
ripple Chebychev, and 0.1 dB ripple, -84 dB stop-band floor
Cauer-elliptic transfer functions. The curves are normalized to the -3
dB cutoff frequencies. |
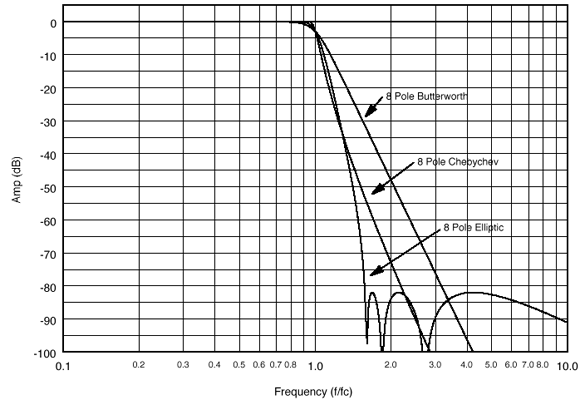
Figure 12
 |
|
Generally,
filters that produce faster roll-off in the transition-band exhibit
poorer phase response and group delay characteristics (See Figure 6).
Phase Filters
For some filter applications it is desirable to preserve a transient
waveform while removing higher frequency noise components from the
signal. If each of the frequency components of the input waveform (from
the Fourier series or the Fourier transform) is phase shifted an amount
linearly proportional to frequency, then they remain in the correct
time relationship and sum together to create, at the output, the
original waveform that was present at the input of the filter, with the
higher frequencies components having been removed by the filter. When a
filter has phase delay that varies linearly with frequency it is called
a Linear Phase
filter. A linear phase filter has a constant group delay, at least
through the pass-band. Amplitude filters provide relatively constant
group delay only from 0 Hz to about the mid pass-band frequency range
peak near fc.
As with amplitude
filters, mathematicians have provided polynomial approximations of an
ideal linear phase transfer function. The most common linear phase
filter is based on Bessel (sometimes called Thompson)
functions. Bessel filters provide very linear phase response and little
delay distortion (constant group delay) in the pass-band. They show no
overshoot in response to step input and roll-off monotonically in the
stop-band. They also exhibit much slower attenuation in the
transition-band than amplitude filters. Figure 13
presents amplitude and delay response curves for an 8-pole Bessel.
Other types of phase filters include, constant-delay (a modified
Bessel), equiripple phase, equiripple delay, and Gaussian transfer
functions. They either have more pass-band amplitude roll-off for only
a small improvement in phase linearity or only slightly less roll-off
in the pass-band at the expense of degrading the phase linearity.
|

Figure 13
 |
|
Compensated Filters
Some applications require filters offering the sharp roll-off
characteristics of amplitude-type filters and the linearity of
phase-type transfer functions. Two techniques, amplitude equalization
and delay equalization, are available to achieve these ends. Both add
complexity to filter design, and have theoretical and practical limits.
Amplitude equalization modifies the amplitude response of phase filters to produce a filter that is sometimes called a constant delay filter. Stop-band zeros on the j axis introduce attenuation notches in the stop-band, but contribute no phase or delay to the pass-band response. Figure 14
shows mirror-image right-half, left-half plane pass-band-zero pairs
that modify amplitude response without additional phase or delay. axis introduce attenuation notches in the stop-band, but contribute no phase or delay to the pass-band response. Figure 14
shows mirror-image right-half, left-half plane pass-band-zero pairs
that modify amplitude response without additional phase or delay.
|
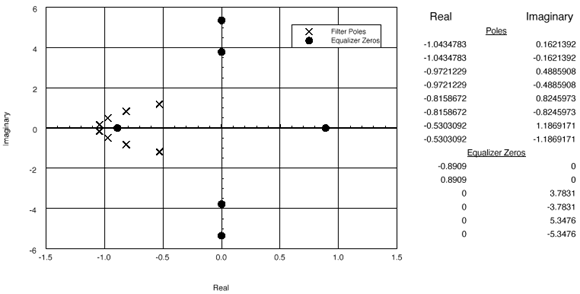
Figure 14
 |
|
Improving
the transition-band roll-off rate, however, does not come free. Adding
zeros also introduces a small amount of step-input overshoot, and
roll-off is no longer monotonic; that is, compensation introduces a
stop-band floor. The j -axis
zeros produce a "soft" or rounded roll-off near the cutoff frequency.
These zeros become the dominant contributors to attenuation-curve
shape, preventing further corner-frequency shape improvement. -axis
zeros produce a "soft" or rounded roll-off near the cutoff frequency.
These zeros become the dominant contributors to attenuation-curve
shape, preventing further corner-frequency shape improvement. This technique can achieve a factor-of-two
improvement in Bessel roll-off to a -80 dB floor, comparable to
Butterworth-filter performance. For comparison, Figure 15 shows the amplitude response of an 8-pole Bessel, an 8-pole, 6-zero constant delay, and a 8-pole Butterworth response.
|
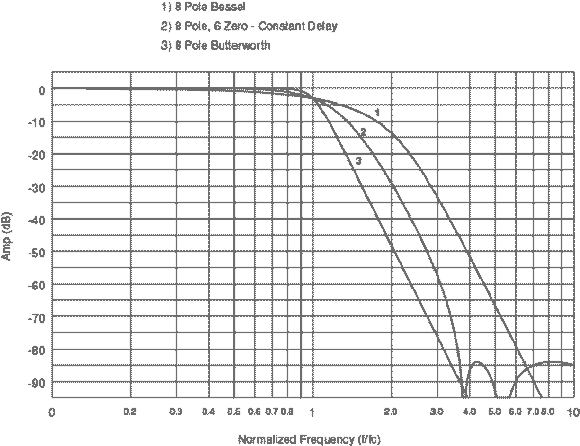
Figure 15
 |
|
Delay equalization
employs additional all-pass (no attenuation) filter sections in cascade
with standard filter sections to modify the phase linearity of
amplitude filters. All-pass filters have left-half-plane poles and
mirror image right-half-plane zeros. The pole and zero locations
determine phase shift, though the added phase shift does not change the
filters amplitude response. Adding phase shift at appropriate places in
the pass-band allows, "straightening out" the phase curve of an
amplitude filter. Each pole-zero pair of an all-pass filter increases
phase shift from approximately 90º at fc to as much as 180º at 10 times fc. Therefore, adding equalizer sections increases total phase shift for the filter/equalizer network.
From
a practical point-of-view, this technique allows filter and system
designers an order-of-magnitude phase-linearity improvement over
conventional amplitude transfer functions. Figure 16
illustrates the group delay of a 6-pole, 4-zero elliptic filter with
and without a two-pole delay equalizer. The equalized plot is flatter
over a larger portion of the pass-band at the expense of an increase in
the amount of delay. The equalization process in this case increases
total phase shift by as much as 360° at the cutoff frequency and by
720° at higher frequencies.
|
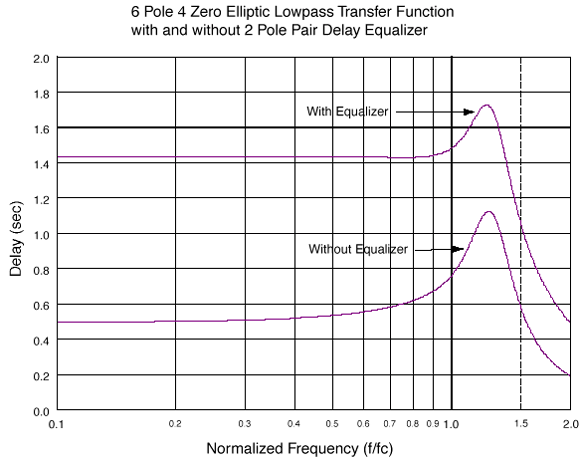
Figure 16
 |
|
The
number and location of poles and zeros in a delay equalizer depend on
the pole configuration of the accompanying filter and the desired
linearity improvement. Therefore, there are no "standard" solutions.
Frequency Devices creates delay-equalization filters based on each
situation and on each customer's specific requirements. OUTPUT SIGNAL ERRORS
Besides inaccuracies of theoretical approximation, the most significant side effects of signal filtering are the following:
Settling time
is not strictly an output signal error because it is mathematically
related to the filter transfer function, but is usually deemed to be an
undesirable filter side effect. All filters serve to delay the input
signal by a certain minimum amount as well as increasing rise and fall
time of any fast changing input signal. A general rule for settling
time is that the more the filter approaches a "brick-wall"
approximation, the longer it will take to settle. Therefore, an
eight-pole filter will take longer to settle than a four-pole filter.
Step Response
for amplitude type filters may exhibit substantial overshoot (ringing)
when presented with a sudden change in voltage amplitude at the filter
input. See Figure 17 for typical 8 pole transfer function step response curves.
|
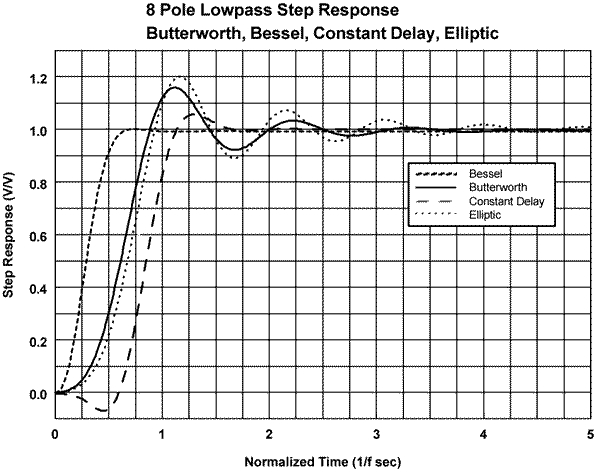
Figure 17
 |
|
DC-offset
adds a voltage directly to an input signal to obtain the output value.
Sophisticated systems may permit calibrating or compensating for this
effect. When evaluating filters and A/D converters, designers must also
consider DC-offset stability with time and temperature to ensure that
compensation circuitry and procedures remain valid regardless of
environmental conditions. For programmable filters, DC offset may vary
with corner-frequency settings. Noise (noise created by both passive
and semiconductor devices) is present at the output of any filter. In
most cases, later filter stages remove stop-band noise from earlier
stages, but they leave noise in the pass-band unaffected. High-Q filter
stages amplify noise near their corner frequencies. In an active
filter, for example, the noise spectrum in the stop-band is usually
flat and low level, resulting largely from the output amplifier. At the
low-frequency end of the pass-band, the noise spectrum is also flat,
but with a magnitude two to four times the level of the stop-band
noise. Near the corner frequency, noise levels peak at magnitudes that
depend on the filter's transfer function. Elliptic filters, which
feature high-Q last stages, produce noise peaks near the corner
frequency of three to five times the level of low-frequency pass-band
noise.
The importance of noise will depend on the
system bandwidth and the level of signals passing through the filter.
In digitizing systems, aliasing folds a frequency spectrum around each
harmonic of the sampling frequency, and because these effects are
additive, achieving the best data accuracy requires reducing
broad-band-noise as much as possible.
Distortion,
harmonics of the input signal's frequency components result from
non-linearity in the filter circuit. These harmonics become inputs to
the A/D converter, which digitizes them with the rest of the signal. As
with broad-band-noise, each low-pass filter stage removes stop-band
distortion components that the previous stage generates. Distortion
levels vary with input-signal frequency, amplitude, transfer function,
and corner frequency.
Total Harmonic Distortion (THD)
is a specification often used as a single number representation of the
distortion present in the output of an active circuit. It is the RMS
sum of the individual harmonic distortions (i.e. 2nd, 3rd,
--- etc.) that are created by the non-linearities of the active and
passive components in the circuit when it is driven by a pure
sinusoidal input at a given amplitude and frequency.
Harmonic
distortion measurement requires a very low distortion sinusoidal input
to the circuit, the removal of the fundamental frequency component from
the output and the measurement of the amplitude of the remaining
harmonics, which are typically 60 to 140 dB below that of the
fundamental.
Spectrum analyzers and FFT
instruments can measure individual harmonic components and can be used
to calculate the THD. For active filters, the THD is usually specified
in dBc (dB relative to the amplitude of the fundamental frequency
component) and at a specific frequency and amplitude (ex. 10Vp-p @
1.0kHz).
An RMS voltmeter can be used to measure
the THD if, the fundamental frequency component can be removed by a
notch filter to a level that is at least an order of magnitude below
the largest harmonic component. However, that measurement will also
include any noise that is within the bandwidth of the meter and is
commonly referred to as the THD + NOISE or THD + N.
At
lower frequencies, amplifiers have sufficient loop gain to reduce
distortion to acceptable levels. For input frequencies near fc,
the filter removes second and higher order harmonics. Above the corner
frequency, filter attenuation reduces the primary signal, which also
reduces the distortion. However, if` the signal frequencies are well
below the corner frequency and the signal has distortion, then that
distortion will also reside in the filter's pass-band. Distortion
components will affect the accuracy of the analog-to-digital signal
conversion.
SELECTING THE RIGHT ANALOG FILTER
Choosing
the correct filter shape for a particular application requires defining
properties of the incoming signal that the filter must remove, as well
as the properties that it must retain. In most situations, there is
some overlap between these two areas, demanding a degree of compromise.
Time Domain Waveform Preservation
Filters
for such applications feature linear phase response in the pass-band,
and must not introduce ringing or overshoot. To preserve the signal
waveform while removing undesired components, the filter must also pass
many harmonics of the incoming signal's base frequency. "Noise"
components that the filter removes must be at substantially higher
frequencies than these necessary harmonics. Phase-derived filters, such
as Bessel or constant-delay (equiripple-phase) and their
amplitude-compensated derivatives, work best in these cases.
High Selectivity in the Frequency Domain
Situations
where removal of undesired components is the overriding concern and
some distortion in the time domain of the signal's shape is of less
importance generally require sharper roll-off filters with Butterworth
or elliptic transfer functions. Spectrum analysis, for example,
involves only the amplitude of each frequency component of the input
signal. Most voice and data transmission also requires integrity only
of amplitudes, as do many forms of modal analysis, which determines
resonant frequencies of structures and objects.
Compromise Filters
Although linear-phase filters preserve critical information, many
applications also require rapid transition-band roll-off. A balance
between these mutually exclusive requirements can often be achieved by
phase-derived types and amplitude-compensated versions of phase
filters. Applications for this approach include determining the
direction of an object or signal source by analyzing the waveform from
one or more receivers.
|
 |
|
 |
|
 |
|
|
|
Electronic Filter Design Guide
|
|
SELECTING A FILTER TECHNOLOGY
In
addition to specifying transfer functions, designers who need signal
filtering must choose among passive, linear-active, switched-capacitor,
and digital-signal-processing (DSP) filter technologies.
Passive Filters
Passive filters contain resistors, inductors and capacitors that
provide polynomial approximations of ideal filters. They often come
packaged in metal cans to reduce inductor magnetic pickup. Corner
frequencies generally range from hundreds of Hertz to many mega-Hertz.
Passive filters require no power (and therefore no power supply) and
generate no DC offset.
Low-frequency
passive filters are large and heavy, and manufacturing them is
expensive. Input signals also undergo "insertion loss" (attenuation) in
the pass-band. The non-linearity of the magnetic materials in the
inductors makes building low-distortion filters of this type difficult.
An engineer who wants to design a custom filter may have trouble
obtaining precision inductive components and tuning the filter to a
specific corner frequency requires considerable expertise. Passive
filter circuits are not easily programmable.
Linear Active Filters
Linear active filters contain resistors, capacitors, and linear
operational amplifiers. Corner frequencies range from 0.001 Hz to 30
MHz. Unlike passive filters, linear-active filters require external
power. Since target systems also require power, this does not generally
present many impediments to designs, however, corner frequencies above
100 kHz call for wide-band amplifiers that demand significant currents.
Some
semiconductor manufacturers have created monolithic-silicon
linear-active filter designs. This approach diffuses or layers internal
capacitors and resistors onto the same silicon substrate as the
semiconductor amplifiers. Attainable capacitor values and stability of
the diffused capacitors and resistors limit this technique's
applicability to higher frequencies, especially for high-order filter
functions.
Switched Capacitor Filters
In
switched-capacitor filters, a switched capacitor simulates a resistor
at an amplifier input, thereby creating an integrator as shown in
Figure 18.
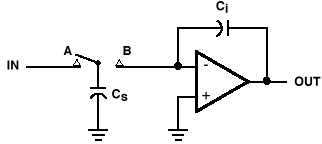
Figure 18
|
 |
|
The circuit momentarily connects to "A", charging capacitor "Cs"
to the input voltage that is present at that moment. It then switches
to "B", dumping the charge onto the amplifier's negative input. The
amplifier then transfers the charge to the integrating capacitor "Ci", where it remains until the next cycle either adds or subtracts charge. The higher the switch frequency, the more often "Ci"
receives charge, which changes the integrator's time constant and
therefore the resulting filter's corner frequency. Varying clock
frequency permits programming filters "on-the-fly". Cascading sections permits constructing multi-pole
filters. In some universal designs, a filter-section's corner frequency
is not an exact sub-multiple of the clock. Cascaded multi-pole versions
of such designs require care to ensure that pole frequencies are
correct. By switching the capacitor at 50 to 100 times the corner
frequency, these filters can attain a good approximation of theoretical
performance.
Since a switched-capacitor filter is
a sampling device, it experiences aliasing errors, frequency components
near the sampling frequency that must be eliminated to ensure accuracy.
Also, this technology produces clock feed-through. Clock feed-through
is an extraneous signal that switched-technology filters create.
Although feed-through resides at 50 to 100 times the filter's corner
frequency, its amplitude can exceed the resolution or noise floor
requirements of the application and can cause additional aliasing
problems. Manufacturers often do not include this factor in their noise
specifications, yet users must make accommodations for clock
feed-through in their system design. Fortunately, its high frequency
makes removal fairly easy with simple second or third-order
linear-active filters.
Switched-capacitor designs
are available as complete filters or as universal building blocks
requiring external resistors to function. Driving clocks may be
internal or external to the filter itself. These filters can be small
(DIPs and SOICs) and inexpensive because they are manufactured as
silicon chips.
|
 |
|
|
|
Electronic Filter Design Guide
|
|
Digital-Signal-Processing Filters (DSP)
Due
to the unique design considerations and requirements associated with
digital filters, along with the ever-changing data conversation (A/D,
DSP, FPGA...) technology, a seperate section of Frequency Devices
Filter Design Guide has been designated for Digital Filters.
Based
on combining ever increasing computer processing speed with higher
sample rate processors, Digital Signal Processors (DSP's) continue to
receive a great deal of attention in technical literature and new
product design. The following section on digital filter design reflects
the importance of understanding and utilizing this technology to
provide precision stand alone digital or integrated analog/digital
product solutions.
By utilizing DSP's capable of
sequencing and reproducing hundreds to thousands of discrete elements,
design models can simulate large hardware structures at relatively low
cost. DSP techniques can perform functions such as Fast-Fourier Transforms (FFT), delay equalization, programmable gain, modulation, encoding/decoding, and filtering.
Programs can be written where:
- Filter weighting functions (coefficients) can be calculated on the fly, reducing memory requirements or
- Algorithms can be dynamically modified as a function of signal input.
DSP
represents a subset of signal-processing activities that utilize A/D
converters to turn analog signals into streams of digital data. A
stand-alone digital filter requires an A/D converter (with associated
anti-alias filter), a DSP chip and a PROM or software driver. An
extensive sequence of multiplication's and additions can then be
performed on the digital data. In some applications, the designer may
also want to place a D/A converter, accompanied by a reconstruction
filter, on the output of the DSP to create an analog equivalent signal.
Figure 19 shows a typical digital filter configuration.
|
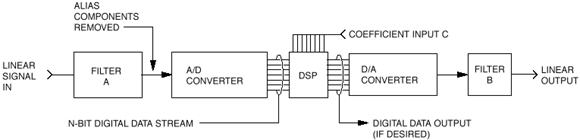
Figure 19 - Typical DSP Filter Configuration
 |
|
Digital filters process digitized or sampled signals. A digital filter
computes a quantized time-domain representation of the convolution of
the sampled input time function and a representation of the weighting
function of the filter. They are realized by an extended sequence of
multiplications and additions carried out at a uniformly spaced sample
interval. Simply said, the digitized input signal is mathematically
influenced by the DSP program. These signals are passed through
structures that shift the clocked data into summers (adders), delay
blocks and multipliers. These structures change the mathematical values
in a predetermined way; the resulting data represents the filtered or
transformed signal. It is important to note that distortion and noise
can be introduced into digital filters simply by the conversion of
analog signals into digital data, also by the digital filtering process
itself and lastly by conversion of processed data back into analog.
When fixed-point processing is used, additional noise and distortion
may be added during the filtering process because the filter consists
of large numbers of multiplications and additions, which produce
errors, creating truncation noise. Increasing the bit resolution beyond
16-bits will reduce this filter noise. For most applications, as long
as the A/D and D/A converters have high enough bit resolution,
distortions introduced by the conversions are less of a problem1.
1.
Theoretically, note that the ratio of the RMS value of a full-scale
sine wave, to the RMS value of the quantization noise (expressed in dB)
is SNR=6.02N + 1.76dB, where N is the number of bits in the ideal A/D
converter.
Although
DSP's rarely serve exclusively as anti-alias filters (in fact, they
require anti-alias filters), they can offer features that have no
practical counterpart in the analog world. Some examples are 1) a
linear phase filter that provides steep roll-off (near brick wall)
characteristics or 2) a programmable digital filter that allows the
signal conditioning to be changed on the fly via software, (frequency
response or filter shape can be altered by loading stored or calculated
coefficients into a DSP program).
Instead of
using a commercial DSP with software algorithms, a digital hardware
filter can also be constructed from logic elements such as registers
and gates, or an integrated hardware block such as an FPGA (Field
Programmable Gate Array). Digital hardware filters are desirable for
high bandwidth applications; the trade-offs are limited design
flexibility and higher cost.
Two Types of DSP’s, Two Types of Math
(1) Fixed-Point DSP and FIR (Finite Impulse Response) Implementations
Fixed-Point
DSP processors account for a majority of the DSP applications because
of their smaller size and lower cost. The Fixed-Point math requires
programmers to pay significant attention to the number of coefficients
utilized in each algorithm when multiplying and accumulating digital
data to prevent distortion caused by register overflow and a decrease
of the signal-to-noise ratio caused by truncation noise. The structure
of these algorithms uses a repetitive delay-and-add format that can be
represented as "DIRECT FORM-I STRUCTURE", Figure 20.
|
 |
|
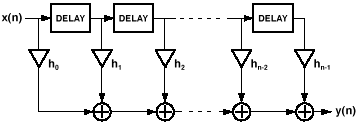
Figure 20 - Direct Form-I Structure
 |
|
FIR
(Finite Impulse Response) filters are implemented using a finite number
"n" delay taps on a delay line and "n" computation coefficients to
compute the algorithm (filter) function. The above structure is non-recursive,
a repetitive delay-and-add format, and is most often used to produce
FIR filters. This structure depends upon each sample of new and present
value data. FIR filters can create transfer functions that have
no equivalent in linear circuit technology. They can offer shape factor
accuracy and stability equivalent to very high-order linear active
filters that cannot be achieved in the analog domain. Unlike IIR
(Infinite Impulse Response) filters (See Item 2 below), FIR filters are
formed with only the equivalent of zeros in the linear domain. This
means that the taps depress or push down the amplitude of the transfer
function. The amount of depression for each tap depends upon the value
of the multiplier coefficient. Hence, the total number of taps
determines the "steepness'" of the slope. This can be inferred from the
structure shown in Figure 20 above.
The number of taps (delays) and values of the computation coefficients (h0, h1,..hn..)
are selected to "weight" the data being shifted down the delay line to
create the desired amplitude response of the filter. In this
configuration there are no feedback paths to cause instability. The
calculation coefficients are not constrained to particular values and
can be used to implement filter functions that do not have a linear
system equivalent. Note: more taps increase the
steepness of the filter roll-off while increasing calculation time
(delay) and for high order filters, limiting bandwidth.
The
filter delay is easily calculated for the above structure. Delay = (0.5
x Taps)/Sampling rate. For example, a 300-tap filter with a sampling
rate of 48 kHz yields a minimum 3.125 milli-second delay [(0.5 x
300)/48 = 3.125 milli-seconds].
Designers must
also be aware of the tradeoffs between phase delay and filter precision
when designing FIR filters. The bad news is that high order FIR filters
have longer delay; the good news is that the phase response remains
linear as a function of frequency. In applications where linear phase
is critical and long phase delay cannot be tolerated, a linear active
Bessel or a constant delay filter may be a better selection.
Two very different design techniques are commonly used to develop digital FIR filters:
|
 |
|
The Window Technique and
The Equiripple Technique.
A. Window's:
The simplest technique is known as "Windowed" filters. This technique
is based on designing a filter using well-known frequency domain
transition functions called "windows". The use of windows often
involves a choice of the lesser of two evils. Some windows, such as the
Rectangular, yield fast roll-off in the frequency domain, but have
limited attenuation in the stop-band along with poor group delay
characteristics. Other windows like the Blackman, have better stop-band
attenuation and group delay, but have a wide transition-band (the
band-width between the corner frequency and the frequency attenuation
floor). Windowed filters are easy to use, are scalable (give the same
results no matter what the corner frequency is) and can be computed
on-the-fly by the DSP. This latter point means that a tunable filter
can be designed with the only limitation on corner frequency resolution
being the number of bits in the tuning word.
B. Equiripple:
An Equiripple or Remez Exchange (Parks-McClellan) design technique
provides an alternative to windowing by allowing the designer to
achieve the desired frequency response with the fewest number of
coefficients. This is achieved by an iterative process of comparing a
selected coefficient set to the actual frequency response specified
until the solution is obtained that requires the fewest number of
coefficients. Though the efficiency of this technique is obviously very
desirable, there are some concerns.
- For
equiripple algorithms some values may converge to a false result or not
converge at all. Therefore, all coefficient sets must be pre-tested
off-line for every corner frequency value.
- Application specific solutions (programs)
that require signal tracking or dynamically changing performance
parameters are typically better suited for windowing since convergence
is not a concern with windowing.
- Equiripple designs are based on optimization
theory and require an enormous amount of computation effort. With the
availability of today's desktop computers, the computational intensity
requirement is not a problem, but combined with the possibility of
convergence failure; equiripple filters typically cannot be designed
on-the-fly within the DSP.
Many
people will use windowing such as a "Kaiser" window to produce good
scalable FIR filters fairly quickly without the worry of
non-convergence. However, if one is interested in producing the highest
performance digital filter for a given hardware configuration, the
iterative Remez Exchange algorithm is worth the test.
Figure 21
illustrates a major advantage that a digital low-pass equiripple FIR
filter can offer designers when solving signal-conditioning problems. FC1 and FS1
are the corner and stop-band frequencies respectively. The typical
number of filter taps used for this -100 dB attenuation example is
around 300. The ratio of FS1 to FC1 is 1.1, an
unheard-of shape factor in the analog world. A slope calculation yields
the fact that an analog filter would have to be a 30th order filter to achieve this performance! Analog filters beyond 10 poles are very difficult to realize and tend to be noisy.
|
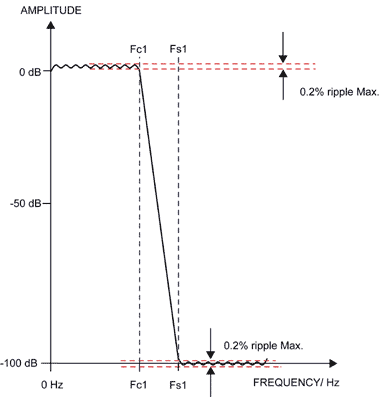
Figure 21 - Low-Pass FIR Filter Template
 |
|
(2) The Floating-Point DSP and IIR (Infinite Impulse Response) Implementations
Like
its name, Floating Point DSP's can perform floating-point math, which
greatly decreases truncation noise problems and allows more complicated
filter structures such as the inclusion of both poles and zeros. This
permits the approximation of many waveforms or transfer functions that
can be expressed as an infinite recursive series.
These implementations are referred to as Infinite Impulse Response
(IIR) filters. The functions are infinite recursive because they use
previously calculated values in future calculations akin to feedback in
hardware systems. The equivalent of classical linear-system transfer
functions can be implemented by using IIR implementation techniques. A
common procedure is to start with the classic analog filter transfer
function, such as a Butterworth, and apply the required transform to
convert the filter equations from the complex S-domain to the complex
Z-domain. The resulting coefficients yield a Z-domain transfer function
in a feedback configuration with a number "n" of delay nodes that is
equal to the order of the S-domain transfer function. These
implementations are referred to as IIR filters because when a short
impulse is put through the filter, the output value does not converge
quickly to zero, but theoretically continues decreasing over an
infinite number of samples. Floating Point DSPs can produce near
equivalent analog filter transforms such as Butterworth, Chebycheff and
elliptic because they use essentially the same mathematical structure
as their analog counterparts. For the same reason, they exhibit the
same or worse non-linear phase characteristics as their analog
counterparts since the equivalent of poles and zeros in linear systems
are reproduced with an IIR, digital filter.
Figure 22
illustrates a bi-quad digital filter structure that computes the
response of a second order IIR transfer function. It has two delay
nodes and the computation coefficients are A1k, A2k, B1k and B2k.
|
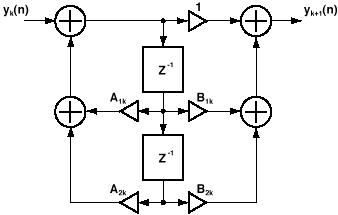
Figure 22 - Bi-quad Digital Filter that Computes Second Order IIR Transfer Function
 |
|
Floating Point processors do have some advantages over Fixed Point processors.
- Specific DSP applications such as IIR filters are easier to implement with floating point processors.
- Floating
Point application code can have lower development costs and shorter
time to market with respect to corresponding programs in a Fixed-Point
format.
- Floating Point representation of data has a smaller amount of probable error and noise.
After all is said, these powerful Floating-Point devices can emulate Fixed-Point processors but at higher hardware cost.
Summary
Complex
digital filter functions involve millions of mathematical operations.
The speed of these operations depends on a variety of factors; DSP chip
speed, filter complexity (number of taps), and the number of bits of
accuracy in each computation. Today, many DSP turnkey and application
specific platforms are available along with development systems for the
savvy engineer, who wishes to do his or her own design. Many computer
programs also exist that can determine the number of taps and the
values of computation coefficients that are required to implement a
specific digital filter performance function. In some cases these
programs output files directly to a PROM burner or Flash Memory,
automatically loading programs (algorithms) into the actual DSP
circuit. One such Software Program is MatLabTM by (The MathWorksTM) which calculates coefficients for designated FIR filters and can also produce IIR filter programs.
Because
of the many hardware and software design options and trade-offs
available in providing signal processing solutions, having the
availability of analog and DSP design and programming expertise along
with application specific Intellectual Property (IP) from one source
can provide a strong argument to the busy design engineer to seek a
turnkey or custom solution from a manufacturer like Frequency Devices.
Examples include:
- Multi-Rate
FIR filters, which can significantly extend low frequency bandwidth
limits and shorten filter delay; both are design limitations of single
rate sampled DSP filter algorithms.
- Ultra low noise and distortion anti-alias and reconstruction filters to 120 dB.
- Low distortion signal generators to 20-bits.
- AD and DA signal converters with -100 dB or better noise floors.
As DSP sample rates continue to increase, the bandwidth and performance of DSP solutions will also increase.
|
 |
|
|
|
Electronic Filter Design Guide
|
|
Digital to Analog Conversion (D/A)
As
with input signals to A/D converters, waveforms created by D/A
converters also exhibit errors. For each input digital data point, the
D/A holds the corresponding value until the next sample period.
Therefore, the output waveform exists as a sequence of steps. This
output, a kind of "sample-and-hold" - is known as a "first-order hold".
Any
step-function approximation of a smooth analog wave such as D/A output
consists of a set of primary-frequency sinusoidals and their harmonics.
To accurately recover the analog signal requires removing these
harmonics, usually with a filter following the D/A. Such a filter
features a very flat amplitude response in the pass-band and a rapid
roll-off above fc. The stop-band floor must be deep enough
to attenuate high-frequency component errors to below an LSB of the
target system's A/D or D/A converter.
Roll-off
need not be as sharp as an anti-alias prefilter, which must push the
target system's useful bandwidth as close as possible to the Nyquist
frequency. Even if the original signal bandwidth is 100% of Nyquist (an
unrealizable goal without serious alias errors), the lowest undesirable
frequency in the D/A output is the second harmonic. For reasons of
convenience, many designers specify the same filter for both anti-alias
and reconstruction. From an attenuation standpoint, however, this
approach represents overkill. In addition, because the step-function
D/A output includes fast rise and fall times, a softer roll-off, more
linear phase filter (Bessel) would work better at this end of the
process because it produces less ringing and overshoot than an elliptic
or similar sharp-roll-off transfer function does.
According to Fourier-transform mathematics, a waveform reconstructed using a first-order hold exhibits an amplitude error (E) that varies as a function of frequency f and the sampling frequency fs, and whose magnitude is given by Figure 23.
|
E =
|
(Sin X)
X
|
, |
where X = |
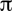 f f
fs
|
|
Figure 23
 |
|
Choosing a Filter Solution
|
Electronic Filter Design Guide
|
|
Choosing
a filter technology is less straightforward than selecting a transfer
function from among Butterworth, Bessel, and Cauer-elliptic. The best
solution depends heavily on the application. To reduce alias errors to
acceptable levels, designers base their filter implementation
selections on the desired bandwidth and accuracy of the target system.
These parameters, along with hardware costs, determine the system's
speed (sampling rate), resolution (number of bits), type of A/D
converter (sigma-delta, successive-approximation, flash, etc.), and
anti-alias/reconstruction filter technology.
Linear-Active Filters serve
applications that require system bandwidths as close as possible to the
sampling frequency, with a sharp cutoff. Simple two or three-pole
versions also serve as anti-alias filters and clock feed-through or
reconstruction filters for systems employing switched-capacitor or DSP
solutions. With active filter technology, very accurate, low frequency
filters in the 2.0 MHz to sub hertz range can be built that are almost
impossible to achieve with other technologies.
Switched-Capacitor
designs work best where cost and space are at a premium. Other criteria
to consider include: when required system accuracy is around 10 to 13
bits, the bandwidth is more than 10 kHz, and where the DC accuracy and
stability specifications of switch capacitor filters are acceptable.
Applications in the multi-megahertz range or requiring power line conditioning (filtering) typically utilize Passive Filters.
This includes snubbers for high-energy inductive or transient
suppression. Also, passive filters must be used when power is not
available, though the user must be willing to tolerate insertion loss
(signal attenuation).
Digital Filters
are used primarily when transfer-function requirements have no
counterpart in the analog world, or when a DSP already resides on the
circuit board to perform other functions.
An example of a digital filter selection limitation is shown in Figure 24.
The pass-band for a high-pass digital filter is limited to the maximum
bandwidth, sampling rate, and word length that the filter order allows.
After that, there is no pass-band! For this example, broadband high
frequency active or passive filters are an obvious alternative.
|
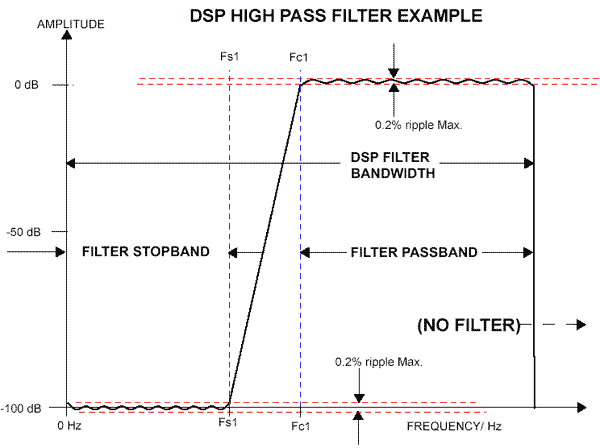
Figure 24
Digital filter selection is the choice or trade-off between Floating
Point DSP - IIR filters and Fixed Point DSP - FIR filters which are
illustrated in the Digital Filter Decision Tree, Figure 25.

Figure 25
 |
|
Whether
you decide on a fixed point FIR or floating point IIR solution, the
world is still analog. In many applications the conversion from analog
to digital and back to analog is a requirement, often with limitations
in bandwidth and design flexibility. One example is range limitation
which is the maximum bandwidth imposed by the sampling when altering
the digital filter frequency. A solution is to adjust the clock, which
forces adjustments in the anti-alias and reconstruction filter,
therefore requiring multiple fixed frequency or programmable filters
(typically not cost effective). Another approach is to adjust the clock
within the DSP by decimation or interpolation; hence the filter shape
can be modified within the filter algorithm. This is called Multi-Rate
filtering and several decimations can be implemented in series to reach
very low frequencies. This Intellectual Property has been well refined
by Frequency Devices engineers.
SHOULD YOU BUILD IT YOURSELF?
Electronic
designers often try to ensure a product's signal integrity by
constructing their own signal processing circuitry. Unfortunately, the
time and money associated with engineering design and assembly efforts
can make the actual cost of such a solution very high. The design may
require a complex arrangement of sensitive components that consume
precious board real estate and compromise system reliability. In
addition, some of these components can generate their own alias signals.
Design
engineers generally understand their own applications very well.
Typically, however, they are not signal-conditioning or
signal-processing experts. Limited experience with integrated analog
and DSP technology often make creating an effective and accurate filter
solution difficult and time-consuming.
On the
other hand, system manufacturers are generally very sensitive to the
cost of purchased solutions. The experts at Frequency Devices have seen
many instances where companies have regarded self-contained signal
conditioning modules and subassemblies as too expensive. Therefore,
engineers design or buy simple, inexpensive alternatives for their
products, hoping that lower cost and typically lower performing
products will be good enough. Such approaches may work, but in many
cases the reduced signal integrity degrades system performance to the
point of unacceptability.
Unfortunately, once
in-house designs do not meet desired performance specifications,
altering the design to incorporate the proper alternative solution or
accepting the degraded signals, usually under extreme time pressures,
generally costs far more than relying on better solutions in the first
place would have. Reinventing the wheel rarely produces the most
effective results.
LET US HELP
Based
on many years of experience with special-purpose signal-conditioning
devices and systems, Frequency Devices offers some of the most advanced
signal-processing products in the industry. We will work with you to
develop specifications that are appropriate to your unique needs,
avoiding either under-specifying or over-specifying in the interest of
controlling cost while maximizing performance.
Whether
prototyping to prove a design, looking for laboratory test equipment or
working with high-volume applications for electronic original equipment
manufacturers and process control, you can rely on Frequency Devices'
data-acquisition, processing, and manipulation solutions for the test
and measurement, aerospace, undersea, navigation, automatic test
equipment, R & D, telecommunications, acoustic, and vibration
markets.
Frequency Devices offers a combination
of turnkey, standard and custom module and subassembly solutions
utilizing both analog and digital signal processing; providing
engineers with choices and solutions consistent with their system or
project requirements.
|
|