Previous page

26. The Capacitor

The capacitor stores electric charge - note that this is entirely different to current & voltage. I'll be explaining this in the dictionary of terms, currently under construction. Once charged, as in the circuit below - the capacitor will store the charge. This charge will not go anywhere (actually, it will slowly leak away - but at an insignificant rate) & can be used to power a circuit for a very short while - lighting a small torch lightbulb for 5 seconds is an impressive feat for a capacitor. They are usually used in a delay circuit - I'll explain why later. Most capacitors are polarity sensitive - ie. they won't work properly if you insert them the wrong way round.

Note that these little dudes will quite happily blow up if you put too much current or voltage through it, or if you connect it the wrong way round (although that only applies to the electrolytic capacitor). They are more than capable of drawing blood, but your limbs are safe & and it's quite difficult to blow them up without trying, as long as you take care when designing your circuits.

Capacitors have a large production spread (see the resistors section if you don't know or can't remember what that is) - it can be up to ±50% .  

A capacitor consists of two metal plates very close together, separated my an insulator. A charge flows onto the plates & remains there when the battery is removed. The charge stored depends on on the capacitance of the capacitor, which is measured on Farads (F). 1F  is a very large capacitance. Below is a table of common capacitances - if you haven't got the symbol font installed on your computer, the first symbol will not display correctly. It should be like a u, with a long tail leading to it from the right. Like a reversed y.

Units in shorthand	Value in Farads	Scientific notation	Written as
1mF	1/1,000,000 F	10-6	microfarads
1nF	1/1,000,000,000 F	10-9	nanofarads
1pF	1/1,000,000,000,000 F	10-12	picofarads

Types of capacitor

Non-electrolytic capacitor

• Fairly small capacitance - normally about10pF to 1mF
• No polarity requirements - they can be inserted either way into a circuit.
• Can take a fairly high voltage.

Variable capacitor

• Adjustable capacitor by turning a knob - similar to variable resistors.
• The maximum capacitance available is about 200pF.
• Used in radios.

Electrolytic capacitor

• Large capacitances - 1mF to 50000mF
• Must be corrected the right way round - the white terminal on the diagram above signifies positive.
• Low voltage rating - about 25V.
• They have a significant leakage current - this means that they will lose the charge stored over time.

Tantalum capacitor

• These have the same properties as the Electrolytic capacitor, but they are physically smaller & have lower leakage. As a result, though, they are more expensive.   

Charging a capacitor

Normally, a capacitor will charge in about a millisecond. However, we can slow it down by putting a resistance in series with it.

In this experiment, there is a new value introduced - the time constant. This is what you get if you multiply the resistance with the capacitance in the following circuit. The actual time, however, will not be this value, due to the production spread. For this experiment, we are seeing how long it takes for the capacitor to charge up to 5V. The switch is in the circuit to drain the capacitor. Note that below we are dealing in microfarads. Note also that s is the symbol for seconds.

Capacitance (mF)	Resistance (M)	Time (s)	Time Constant
100	1	100	100
100	0.1	10	10
100	0.47	45.5	47
330	1	535	330
33	3.3	97	99

The capacitor charges rapidly at first, then slows down. The time to taken to charge is proportional to capacitance * resistance, also known as C*R.

Timing circuit

The bulb comes on a short time after the switch is opened, when the capacitor voltage reaches 0.7V.

27. The bistable (or latch)

This is advanced logic - if you don't know about the normal logic, you don't have a hope of understanding this. So go & get acquainted by clicking here.If you feel you already understand logic, or are too stubborn to take my advice, then continue. From now on, it gets a little more complicated.

The latch is a handy piece of logic & circuitry to know - but it's very confusing if you try to figure it out. It's easier to explain if we use an example. So let's use a burglar alarm.

OK. You are a person who has decided to create a burglar alarm for his house. You're going to get it to trigger by placing a touchpad under the doormat, that gives a logic 1 when trodden on. You've already designed the logic circuit to set the alarm off if the circuit receives a logic 1 from the touchpad AND a logic 1 from the control panel when it is set (another system that you have already designed). So you wire up your ciruit, set it, and go out. By an astonishing coincidence, a burglar breaks in. And by another astonishing coincidence, the burglar breaks in using the door. he takes a step in, & treads on the touchpad. Your AND circuit will give a logic 1, and set the alarm off. "Oh dear" thinks the burglar, and he runs off.
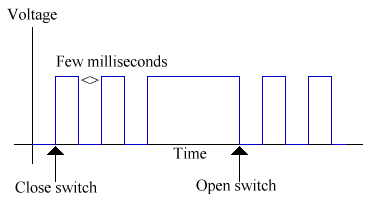
As soon as he takes his foot off the pad, the logic gate will automatically give a logic 0, because it no longer recieves a logic 1 from both inputs. Thus the alarm promptly turns itself off. "Yipee!" thinks the burglar, steps over your doormat, and rids you of your worldly possessions.

So, how do you prevent this happening? You need the alarm to stay on when the AND gate gives a 0 when it was previously given a 1. You do this using a latch, which will 'latch on' when there is a logic 1 to it. It's a bit like those switches, which stay down until you press it again. Before we look at the two types of latch, you must learn about a new symbol - Q with a bar over it. I can't type it, but you'll see it on the diagrams below. It means NOT Q.

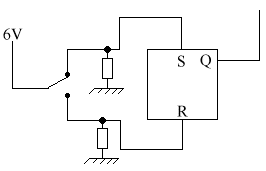
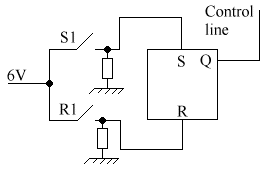
From NOR gates

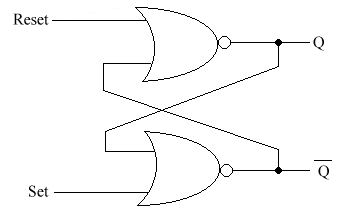
If R = 1 & S = 0 then Q = 0, ie. It is reset.
If R = 0 & S = 1 then Q = 1, ie. It is set.
If R = 0 & S = 0 then Q can be either 0 or 1, depending on whether R or S was previously equal to 1. This is known as the memory state.

From NAND gates

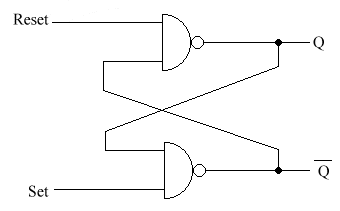
If R = 1 & S = 1 then Q = 0 or 1 - it is in the memory state.
If R = 0 & S = 1 resets Q to 0
If R = 1 & S = 0 sets Q to 1

This is known as sequential logic. This means that the output value depend on the previous states of the input.

The memory state stores the previous output. For example, if Q = 1 in a NOR gate from R = 0 and S = 1, and then R & S were both set to 0, the output would remain 1. But if the previous state was a 0, from a R = 1 and an S = 0, and then it was set to the memory state, it would remain 0. This is how computer memory works.

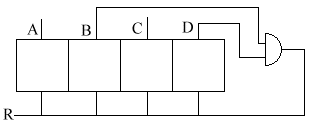
The Memory Register

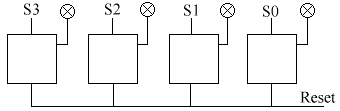
Before we get into this, the little circles with a cross inside them are indicators.They're just symbolic representation - don't use them in cicuit diagrams. The only reason they're used here is for simplicity. All the S's are the Sets.

In this, we are using 4 bistables. We want to remember the number 5, which in binary (if you don't understand binary, click here) is 0101. What do we have to do to set it to 0101? The not very perceptive would say that you apply a logic 1 to S0 &S2. But what if S1 & S3 were previously set to 1? Then your circuit will read 15. Which is not what we want. So, we have to reset all bistables, apply logic 1 to S0 & S2, and set all the S's to 0.

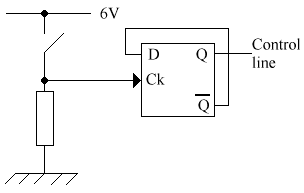
The D-Type (Data Type) bistable  

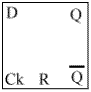
This is also sometimes known as a flip-flop. It has a couple of new things that you haven't seen before: A clock (Ck) & a Data (D) input. Q will become equal to D on the falling edge of the clock pulse (ie. When the Ck goes from 1 to 0).

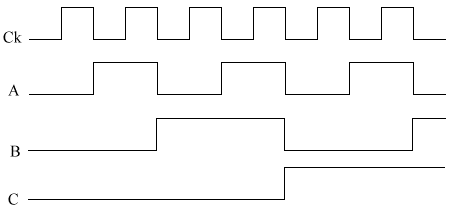
The timing diagram.

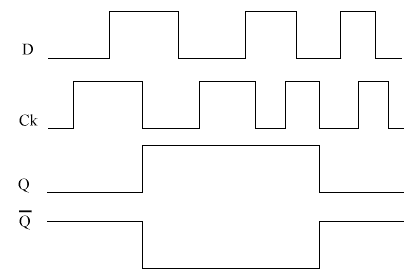
We draw in the Ck & the D, and presume that Q starts at 0. We then draw the predictions (See example below).

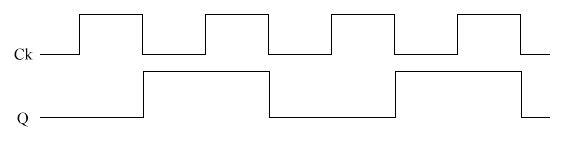
What happens if Q bar is connected to D?

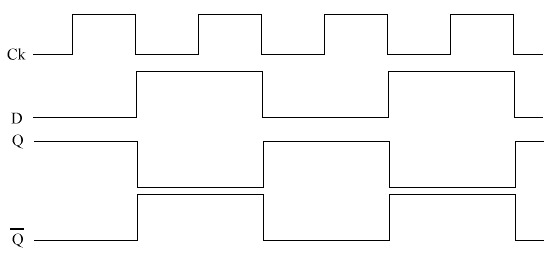
What happens is that whenever Ck goes from 1-0, Q changes state. This is known as a toggle. Note that this is happening at half the frequency of the clock.

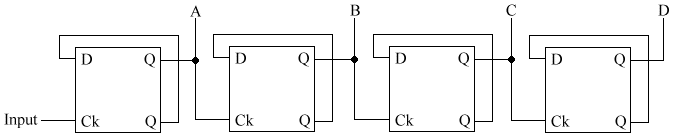
Counting circuit

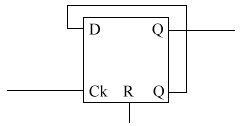
As many of these blocks can be added as neccessary(see below).

The Binary up counter

Ck Pulse	A	B	C	D
0	0	0	0	0
1	1	0	0	0
2	0	1	0	0
3	1	1	0	0
4	0	0	1	0

A changes when the Ck goes to 0, B changes when A goes to 0, C changes when B goes to 0, and D changes when C goes to 0. Note that this is not when A=0, but when it goes to 0 - ie. it was previously a 1. Below is the timing diagram.

The BCD counter

Remember Binary Coded Decimals? You can make any binary up counter count to whatever you want, by using a logic system to give a logic 1 to the resets when it gets to the number you want. For example, here we want a  BCD counter. The boxes are just a binary up-counter system, with A, B, C, & D being the outputs. So we need it to reset when it reaches 1010 (10 in binary). 

Uses of bistables

The main applications of bistables are either in a counter or a timing circuit. They are also used often in logic circuits. We shall look at a Stopwatch. But before we do, we'd better look at contact bounce.

Contact Bounce

Contact bounce is when the switch contacts give several 1 to 0 signals to a clock input. When you close a switch, they don't just stop. They bounce a bit, connecting & disconnecting. Like when you drop a tennis ball. It doesn't hit the ground & stop - it bounces. This is a nuisance, as it means that if we are using a switch to provide an input for a counter, one press of the switch can send multiple signals. Slide switches are a great offender for contact bounce - as the contacts slide over one another, they send many 1 to 0 signals. This is a serious problem, so it cannot be ignored.

This is what happens when the swtich is pressed in the circuit:

As you can see, this is not good for a clock input. So, we could use this circuit:

This switch solves the problem of contact bounce.

Stopwatch using a pulse generator (astable)

An astable gives pulses. We will use a 1Hz pulse generator, as it gives one pulse per second. We will deal with astables in the next section. Let's start off with the systems diagram for the stopwatch:

We need to make the 10s digit count on a scale of 6, as there are 60 seconds in a minute. We need the AND gate & control line because of contact bounce, so we cannot use a switch The idea of it is that when the control line gives 1 AND the pulse generator pulses, a pulse is given from the AND gate. This system acts as a start & stop. We could use this circuit for the control line:

The strange new symbol at the base of the resistor is a ground. It provides a way for the voltage to leave, like a 0V line. This still won't work tht well, as it does not solve the problem of contact bounce - many signals will be sent to the AND gate. it will work, but not reliably. And the user has to hold the button down to time something. So we could use this circuit:

This circuit is a lot better. When we press the switch S1 then the control line gives a 1. When we press the swich to R1, then the control line gives a 0. This is a more efficient system, as it does not require the user to hold down a button. But there is a better solution:

This circuit is a toggle - whenever the switch is pressed, the output of the control line changes. It is a much better solution to our problem.

28. The Astable (or pulse generator)

The astable is not stable in any state. This means that it continually changes between a giving a logic 1 & a logic 0. This is a diagram of a wave from an astable:

• Pulse width is the time that the output is high.
• Pulse spacing is the time that the output is low.
• The Time Period is the time for a complete cycle.
• Frequency is the number of oscillations per second. It is 1 / Time Period. It is measued in Hertz, or Hz.
• The mark to space ratio is the pulse width / pulse spacing.

29. The Cathode Ray Oscilloscope (CRO)

 

An oscilloscope is used to measure high frequencies & voltages of high frequencies. Here is a picture of a wave. This is known as the trace:

There are many controls on an oscilloscope. Here are the most important ones:

• Vertical calibration - this sets how many volts there are per division on the screen. In the picture above, we have a vertical calibration of 0.5V/div. The trace is 2 div. high, so it has a 1V peak voltage.
• Time Base - this is the horizontal calibration, or where the spot would move uniformly across the screen. eg. 2ms/div. Our trace is 8 divisions/cycle. The time period = 8 div * 2ms/div = 16ms. Frequency = 1/T = 1/0.016 = 62.5 Hz.
• Trigger - gives a stable trace. It ensures that each scan of the screen starts at the same point of the waveform.

 

30. The 555 timer as an astable

The 555 timer is a very versatile chip. Here you will learn how to use it as an astable.

The 555 comes in a Dual In-Line (DIL) Package. This means that it has two rows of pins. Here is a picture of a 555, much enlarged. The text is the name of the pin and the number is the pin number.

The more observant of you will have noticed the semicircle at the top and the little blck circle in the top right. This is to tell you where the top of the chip is. When you buy the chip, it is only about 1 cm long, so there is no room to write the pin names. So the chip maker cuts a little semicircular bit out at the top. Sometimes there is also a black dot to show where pin 1 is.

To use an astable, you need to use this circuit:

 

You don't need to know how this circuit works, but it is to do with the capacitor charging until it needs to discharge through the threshold and the trigger. You can change the size of the pulses by changing the resistances and the capacitance of the capacitor on the bottom right.

The graph above is an illustration of a 555 output. There are some formulas for a 555. R1 is the top resistor, R2 the bottom, and C the capacitor in the bottom right:

Ton = 0.7 * (R1 + R2) * C
Toff = 0.7 * R2 * C
Time period = ((R1 + 2R2) * C) / 1.44

Next page