Basic Logical Functions and Gates

Direct links to other logic pages:
Combinational Logic:
[Basic Gates]
[Derived Gates]
[The XOR Function]
[Binary Addition]
[Multiplexer]
[Decoder/Demultiplexer]
Sequential Logic:
[RS NAND Latch]
[Clocked RS Latch]
[RS Flip-Flop]
[JK Flip-Flop]
[D Latch]
[Flip-Flop Symbols]
Counters:
[Basic 4-Bit Counter]
Registers:
(Coming Soon)
Return to Digital index page.
Return to Play-Hookey Home Page.

While each logical element or condition must always have a logic value
of either "0" or "1", we also need to have ways to
combine different logical signals or conditions to provide a logical
result.
For example, consider the logical statement: "If I move the switch
on the wall up, the light will turn on." At first glance, this seems
to be a correct statement. However, if we look at a few other factors, we
realize that there's more to it than this. In this example, a more
complete statement would be: "If I move the switch on the wall up
and the light bulb is good and the power is on, the light
will turn on."
If we look at these two statements as logical expressions and use
logical terminology, we can reduce the first statement to:
Light = Switch
This means nothing more than that the light will follow the action of
the
switch, so that when the switch is up/on/true/1 the light will also be
on/true/1. Conversely, if the switch is down/off/false/0 the light will
also be off/false/0.

Looking at the second version of the statement, we have a slightly more
complex expression:
Light = Switch and Bulb and Power
Normally, we use symbols rather than words to designate the and
function that we're using to combine the separate variables of Switch,
Bulb, and Power in this expression. The symbol normally used is a dot,
which is the same symbol used for multiplication in some mathematical
expressions. Using this symbol, our three-variable expression becomes:
Light = Switch  Bulb
Bulb
 Power
Power

When we deal with logical circuits (as in computers), we not only need
to deal with logical functions; we also need some special symbols to
denote these functions in a logical diagram. There are three fundamental
logical operations, from which all other functions, no matter how complex,
can be derived. These functions are named and, or, and
not. Each of these has a specific symbol and a clearly-defined
behavior, as follows:


|
|
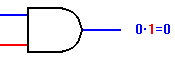
The AND Gate The AND gate implements the AND function. With the gate
shown to the left, both inputs must have logic 1 signals applied to them
in order for the output to be a logic 1. With either input at logic 0, the
output will be held to logic 0.
If your browser supports the Javascript functions required for the
demonstrations built into this page, you can click the buttons to the left
of the AND gate drawing to change their assigned logic values, and the
drawing will change to reflect the new input states. Other demonstrations
on these pages will work the same way.
There is no limit to the number of inputs that may be applied to an AND
function, so there is no functional limit to the number of inputs an AND
gate may have. However, for practical reasons, commercial AND gates are
most commonly manufactured with 2, 3, or 4 inputs. A standard Integrated
Circuit (IC) package contains 14 or 16 pins, for practical size and
handling. A standard 14-pin package can contain four 2-input gates, three
3-input gates, or two 4-input gates, and still have room for two pins for
power supply connections.
|


|

|
The OR Gate The OR gate is sort of the reverse of the AND gate. The OR
function, like its verbal counterpart, allows the output to be true (logic
1) if any one or more of its inputs are true. Verbally, we might say, "If
it is raining OR if I turn on the sprinkler, the lawn will be wet." Note
that the lawn will still be wet if the sprinkler is on and it is also
raining. This is correctly reflected by the basic OR function.
In symbols, the OR function is designated with a plus sign (+). In
logical diagrams, the symbol to the left designates the OR gate.
As with the AND function, the OR function can have any number of
inputs. However, practical commercial OR gates are mostly limited to 2,
3, and 4 inputs, as with AND gates.
|



|
|
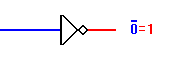
The NOT Gate, or Inverter The inverter is a little different from AND and OR gates in
that it always has exactly one input as well as one output. Whatever
logical state is applied to the input, the opposite state will appear at
the output.
The NOT function, as it is called, is necesasary in many applications
and highly useful in others. A practical verbal application might be:
The door is NOT locked = You may enter
The NOT function is denoted by a horizontal bar over the value to be
inverted, as shown in the figure to the left. In some cases a single quote
mark (') may also be used for this purpose: 0' = 1 and
1' = 0. For greater clarity in some logical expressions, we will
use the overbar most of the time.
In the inverter symbol, the triangle actually denotes only an
amplifier, which in digital terms means that it "cleans up" the
signal but does not change its logical sense. It is the circle at the
output which denotes the logical inversion. The circle could have been
placed at the input instead, and the logical meaning would still be the
same.
|

The logic gates shown above are used in various combinations to perform
tasks of any level of complexity. Some functions are so commonly used that
they have been given symbols of their own, and are often packaged so as to
provide that specific function directly. On the next page, we'll begin our
coverage of these functions.
 Back to the Play-Hookey main page.
Back to the Play-Hookey main page.
 Bulb
Bulb
 Power
Power Bulb
Bulb
 Power
Power